1.
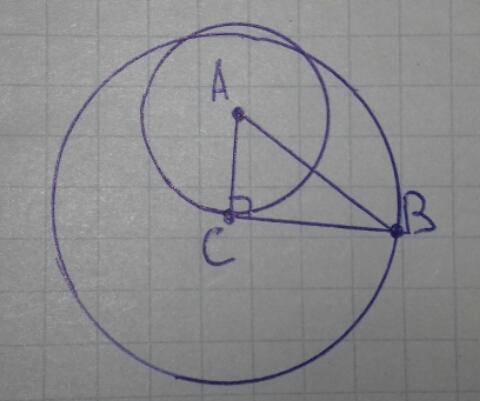
BC⊥AC как катеты прямоугольного треугольника.
BC∩AC = C; AC - радиус окружности с центром A.
Получаем, что BC перпендикулярно радиусу (AC) окружности с центром A и BC пересекает этот радиус в точке (C), принадлежащей той же окружности, поэтому BC это касательная.
2.
AB пересекает окружность (C, CB) в точке B, а CB это радиус той же окружности, проведёный к точке B. Если AB было бы касательной, то AB⊥BC, но это не возможно т.к. AB - гипотенуза, а BC - катет одного прямоугольного ΔABC. Поэтому AB не может быть касательной.
Обозначим точки касания окружности с катетами М - на ВС, К - на АС, и соединим их с центром О окружности.
ОМ=ОК=ВК=МВ=R
∆ АВС~ ∆ MOC, - оба прямоугольные, МО|| АВ, угол С - общий.
Тогда ВС:СМ=АВ:ОМ
28:(28-R)=21:R
28R=588-21R
49R=588 откуда R=12