Sтрапеции = (a+b)*h/2
т.к. трапеция равнобедренная AB=CD=12
проведем две высоты BK и CM, треугольники ABK и CMD равны (не только подобны по двум углам, но и равны) => AK=MD, угол BAK=180-120=60 (т.к. основания трапеции || ), => угол ABK = 180-90-60=30
высота трапеции AK = 1/2 * AB = 12/2 = 6 (как катет, лежащий против угла в 30 градусов)
по т.Пифагора BK^2 = 12*12 - 6*6 = (12-6)(12+6) = 6*18 = 3*2*2*9
h = BK = 2*3*корень(3) = 6*корень(3)
ВС = AD - 2*AK = 16 - 2*6 = 4
Sтрапеции = (16 + 4) * 6*корень(3)/2 = 60корень(3)
первая задача) углы BCA=ACD (AC---биссектриса)
углы BCA=CAD (как накрестлежащие при параллельных основаниях трапеции и секущей AC)
получили треугольник ACD с равными углами DAC=ACD => AD=CD=16
т.к. трапеция равнобедренная MD=(AD-BC)/2 = 12/2=6
по т.Пифагора высота = корень(16*16-6*6) = корень((16-6)(16+6)) = корень(10*22) =
корень(5*2*2*11) = 2корень(55)
Sтрапеции = (16 + 4) * 2*корень(55)/2 = 20корень(55)
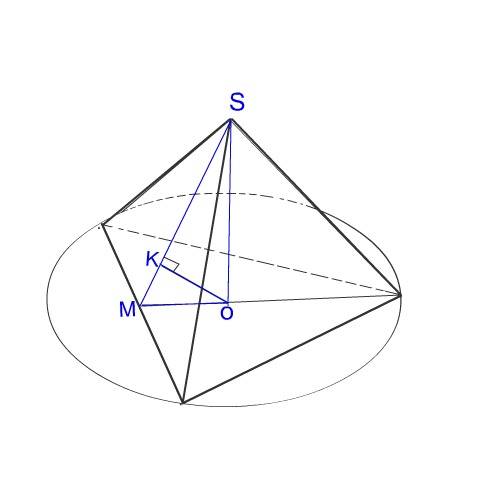
Расстояние от центра описанной около основания этого тетраэдра окружности до грани - перпендикуляр к этой грани.
На рисунке - это отрезок ОК.
Центр описанной около правильного треугольника окружности ( а грани правильного тетраэдра - правильные треугольники) лежит на пересечении высот треугольника на расстоянии одной трети высоты от стороны.
Найдем высоту треугольника по формуле
h=a√3):2, а так как а=1,то
h= √3):2
ОМ=√3):2):3=√3):6
Так как все грани правильного тетраэдра равны,
SM равна h=√3):2
Расстояние КО будем находить из прямоугольного треугольника SОМ
Применим теорему:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Здесь этот катет - ОМ
ОМ²=МК·SM
(√3):6)²=МК·(√3):2)
МК=3/36:(√3):2)=6/36):√3=1/6√3
ОК²=МО²-КМ²
ОК²=3/36 -1/108=9/108-1/108=8/108=2/27=6/81
ОК =√(6/81)=√6):9
1) Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒ NC:СВ=6:3, и MC:СА=8:4. Одна из формул площади треугольника S=a•b•sinα•1/2, где а и b - стороны, α- угол между ними. Sin45°=√2/2, Тогда Ѕ(ACN)=6•4•√2/2=6√2. Медиана делит площадь треугольника пополам, три медианы делят его на 6 равновеликих треугольника. S(MNK)=6•Ѕ(ACN)=36√2 (ед. площади)
2) В ∆ АЕС по теореме синусов АЕ:sin∠С=АС:sin∠АЕC. Сумма углов треугольника 180°. В ∆ АВС ∠С =180°-(α+ β). ∠АЕС=180°-γ. ⇒ m:sin(180°-α- β)= =AC:sin(180°-γ), откуда АС=m•sin(180*-γ)/sin(180*-α-β).
3) Диагонали параллелограмма точкой пересечения делятся пополам. ⇒ В треугольнике МNP отрезок МО - медиана. Формула медианы произвольного треугольника М=(√(2a²+2b²-c²):2, где а и b - стороны, с - сторона, которую медиана делит. ⇒ МС=2МО=√(32+72-28)=2√19 ед. длины.
Или
Из ∆ МNP по т.косинусов NP²=MN²+MP²-2•MN•NP•cosNMP ⇒ MP²=16+36-48•cosNMP ⇒ cosNMP=(28-52):(-48)=1/2
По т.косинусов МК²= MN²+NK²-(-2•MN•NK•cos∠MNK). Сумма соседних углов параллелограмма 180° (т.к. МР||NK, MN - секущая, угол NMP и угол MNK- внутренние односторонние). ⇒cosMNK= - cosNMP ⇒ МК=√(52+24)=2√19 (ед. длины)