Задание 2
Дано:
DO = OC
AO = OB
Доказать, что треугольник CAO равен треугольнику DBO
Доказательство
Рассмотрим треугольник CAO и треугольник DBO
DO = OC - по условию
AO = OB - по условию
угол DOB равен углу AOC, т.к. углы вертикальны
следовательно треугольник CAO равен треугольнику DBO по 1 признаку равенства треугольников
ч.т.д
Задание 4
Дано:
AD- биссектриса
угол ADB = углу ADC
Доказать, что AB = AC
Доказательство
Рассмотрим треугольник ABD и треугольник ACD
угол ABD = углу ADC - по условию
угол BAD = углу DAC - т.к AD - биссектриса
AD - общая
следовательно треугольник ABD = треугольнику ACD по 2 признаку равенства треугольников
следовательно AB = AC
ч.т.д
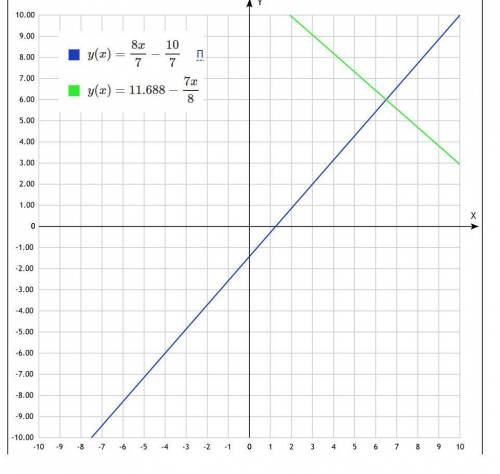
1) уравнение АВ
y=ax+b
подставлю точки
2=3a+b
10=10a+b
система это
из первого b=2-3a и во второе
10=10a+2-3a; 8=7a; a=8/7
подставлю в первое a и найду b
2=3*8/7+b; b=2-24/7=(14-24)/7=-10/7
тогда уравнение прямой AB
y=8x/7-10/7
7y=8x-10
8x-7y-10=0
2) уравнение перпендикулярной линии к АВ имеет вид
7x+8y+c=0 (8*7-7*8=0-скалярное произведение нормалей равно 0 у перпендикулярных прямых)
чтобы вычислить с-надо подставить в него координаты середины О отрезка АВ, через которую проходит искомая прямая
O((3+10)/2;(2+10)/2)=(6.5;6)
7*6.5+8*6+c=0
45,5+48+c=0
c=-93.5
7x+8y-93.5=0-уравнение искомой прямой
21корень из 54/44=12.3