
76°
Объяснение:
Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник - равнобедренный.
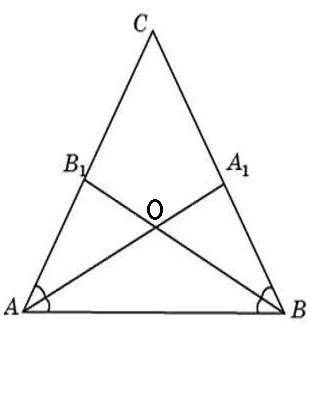
1) Рассмотрим ΔАСВ.
∠С =28°, ∠А = ∠В по условию. Т.к. сумма углов 28° Δ-ка равна 180°, то?
∠А + ∠В + ∠С = 180°, откуда
∠А + ∠В = 180° - ∠С = 180° - 28° = 152°. Но ∠А = ∠В по условию, следовательно,
∠А = ∠В = 152°/2 = 76°
2) т.к. ∠А = ∠В , а АА₁ и ВВ₁ - биссектрисы этих углов, то
∠В₁АО = ∠ОАВ = ∠А₁ВО=∠ОВА = 76°/2 = 38°
3) Рассмотрим ΔАОВ.
∠ОАВ = ∠ОВА =38°, тогда
∠АОВ = 180° -2*38° = 180° -76° = 104°
4) ∠АОВ и ∠АОВ₁ - смежные углы, их сумма = 180°, значит,
∠АОВ₁ = 180°-104° = 76°
Длину отрезка АВ можно найти по формуле расстояния между точками:
AB = √((x₁ - x₂)² + (y₁ - y₂)²)
AB = √((- 3 - 1)² + (2 - (- 5))²) = √(4² + 7²) = √(16 + 49) = √65
Координаты середины отрезка находятся по формуле:
x = (x₁ + x₂)/2
y = (y₁ + y₂)/2
x = (- 3 + 1) / 2 = - 1
y = (2 + (- 5)) / 2 = - 1,5
Если точка С - середина отрезка АВ, то С(- 1 ; - 1,5)