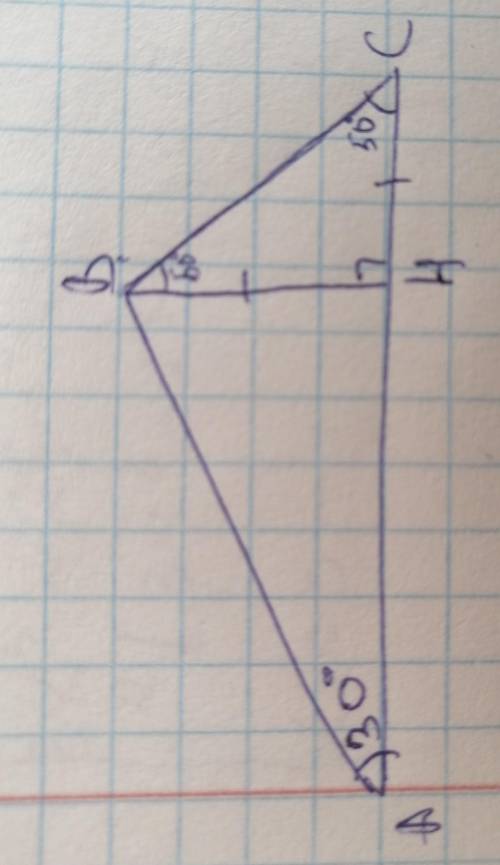
АС=10 ВС=11 АВ=17
Объяснение:
ВНперпендикулярен АС
ТреугольникВНС- равнобедр, т.к. уголС=углуНВС=50°
ВН=НС
пумть:
ВН=х
АС=10
АН=10-х
tg30°=BH/AH=x/10-x
x(10+tg30°)=tg30°
x=tg30°/10+tg30°=1/корень3/10+1/корень3=1/10+корень3
ВН=1/10+корень3=СН
sin50°=BH/BC(0.8рад)
BC=BH/sin50°=1/10+корень3 : 8/10=5/40+4корень3(примерно 0,11)
ВС=11
sin 30°=BH/AB
AB=BH/sin30°=1/10+корень3 : 1/2= 2/10+корень3(примерно 0,17)
АВ=17
наименьшая сторона АС
(чертёж на быструю руку)
На счёт этой задачи не уверена правильный ли ответ. Было бы лучше есть место 50° было 45°.
пусть х - коэффициент пропорциональности.
Из условия ясно, что АВ=ВС=СD=AD=А₁В₁=В₁С₁=С₁D₁=A₁D₁=3x
CC₁=AA₁=4x; АС=√(АВ²+ВС²)=√(9х²+9х²)=3√2*х
A₁B=√(AA₁²+AB²)=√(16x²+9x²)=5x
Диагональное сечение прямоугольник А₁С₁СА, его площадь равна
АС*СС₁=3√2х*4х=12√2х²
Найдем х
(ВС+СС₁+D₁C₁+D₁A₁+A₁B)=3x+4x+3x+3x+5x=36⇒x=36/18=2
тогда площадь диагонального сечения равна 12√2х²=48√2/см²/
Верный ответ а) 48√2 см²
Приношу извинения. что не могу использовать приложение/не работает/, чтобы изобразить параллелепипед, но это совсем легко, в любом учебнике он изображен стандартно.
(то есть у треугольника ABD известны все три стороны AB = 18;)
С ходу в голову приходит воспользоваться теоремой косинусов, и тем, что углы ADB и CDB - дополнительные. Если (для максимальной краткости записи) обозначить 2*cos(Ф) = z; где Ф - это угол CDB; и DC = x; то
12^2 + 12^2 + 12*12*z = 18^2;
12^2 + x^2 - 12*x*z = 18^2;
откуда конечно можно найти x = DC;
дальше техника. Вместо того, чтобы находить из первого уравнения z и подставлять во второе, можно заметить, что
x^2 - 12*x*z = 12^2 + 12*12*z;
или
x^2 - 12^2 = 12*(x + 12)*z;
12*z = x - 12; если это подставить в первое уравнение, получится
12^2 + 12^2 + 12*(x - 12) = 18^2 = 12*27;
12 + 12 + x - 12 = 27;
x = 15;
Все это хорошо, но есть совсем элементарное решение.
Очевидно, что треугольники ABD и ABC подобны - это равнобедренные треугольники с одинаковыми углами при основаниях.
Треугольник ABD подобен треугольнику (2,2,3) с коэффициентом 6, то есть (12,12,18); а треугольник ABC имеет боковую сторону 18, то есть коэффицент подобия 9 с тем же треугольником (2,2,3) то есть его основание AC = 27; откуда DC = 15;