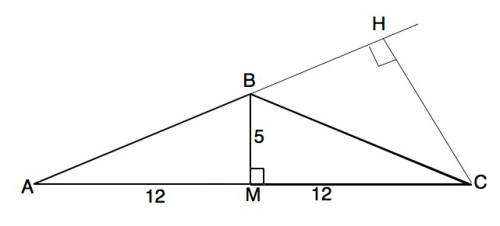
Медиана равнобедренного треугольника, проведенная к основанию, является и его высотой. АМ=МС=24^2=12 см, ВМ⊥АС. Из прямоугольного ∆ ВМС по т.Пифагора гипотенуза ВС=√(BM²+MC²)=13 см. Из прямоугольного ∆ ВМС синус угла при основании ВМ:ВС=5/13.
Проведем высоту СН к стороне АВ. Высота тупоугольного треугольника, проведенная из острого угла, проходит ВНЕ его и пересекает продолжение стороны. Треугольник АНС прямоугольный ( т.к.СН высота). АС - гипотенуза. Угол А=углу С ( ∆ АВС равнобедренный). Синус угла А=5/13. Искомая высота – катет СН=АС•sinA=24•5/13=9³/₁₃
У равнобедреннего треугольникаАВ=ВС.
Пусть АС=х см, тогда АВ=АС=х+9
Р(АВС)=АС+АВ+ВС
Р(АВС)=2(х+9)+х=42
2х+18+х=42
3х = 24
х=8=АС
Тогда АВ и ВС = 8+9 = по 17 см каждая
(проверка 8+17+17 = 42 см)