Два возможных случая:
1) 
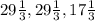
2) 
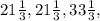
Объяснение:
Т.к. треугольник равнобедренный, то по определению имеет 2 равные боковые стороны.
Случай 1. Пусть основание меньше боковой стороны, тогда основание = x, а боковые стороны x + 12. Периметр - это сумма всех сторон, так что составим уравнение:
x + (x+12) + (x+12) = 76
3x + 24 = 76
3x = 76 -24
3x = 52
x = 52: 3 =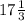 
- основание, значит боковая сторона = x + 12 =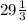 
Случай 2. Пусть основание больше боковой стороны, тогда основание = x, а боковые стороны x - 12.
Составляем уравнение
x + (x-12) + (x-12) = 76
3x - 24 = 76
3x = 76 + 24
3x = 100
x = 100:3 =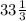 
, ⇒ боковая сторона = x - 12 =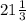 
Доказательство:
1) тр АВЕ = тр СДК (по двум сторонам и углу м/д ними), т к в них
АВ=СД (АВСД- пар-мм)
АЕ=СК ( по условию)
уг КСД= уг ЕАВ как внутр накрестлежащие при AB||СД и секущ АС
следовательно ВЕ=ДК
2) тр АЕД = тр СКВ (по двум сторонам и углу м/д ними), т к в них
АД=СВ (АВСД- пар-мм)
АЕ=СК ( по условию)
уг ЕАД= уг КСВ (как внутр накрестлежащие при AД||СВ и секущ АС
следовательно ВК=ДЕ
3) ЕВКД - параллелограмм по признаку из пп. 1;2