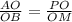
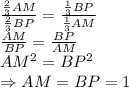
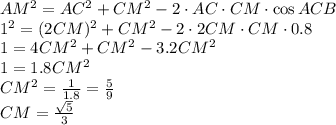
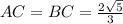
дано: ab=ad,
∠bac=∠dac
доказать: ∆abc=∆adc
доказательство:
1) ab=ad (по условию)
2) ∠bac=∠dac (по условию)
3) ac — общая сторона.
следовательно, ∆abc=∆adc (по двум сторонам и углу между ними)
дано:
ao=bo,
co=do
доказать: ∆aoc=∆bod.
доказательство:
определяем те элементы, о равенстве которых известно по условию :
1) ao=bo (по условию)
2) co=do (по условию).
3) ∠aoc = ∠bod (как вертикальные).
дано:
ab=ac,
af=ak
доказать: ∆abk=∆acf
доказательство:
1) ab=ac (по условию)
2) af=ak (по условию)
3) ∠a — общий.
следовательно, ∆abk=∆acf (по двум сторонам и углу между ними).
вычислите периметр равнобедренного треугольника авс, если периметр треугольника adc равен 18 cм, и cd = 6 cм и ad = bd (fig.5)
доказательство:
периметр треугольника adc = ac + cd + ad = 18 ⇔ ac + 6 + ad = 18 ⇔ ac + ad = 12
потому что ac = bc (треугольники являются равнобедренными) и ad = db, следовательно ac + ad = db +bc = 12
периметр треугольника abc = ab + ac + bc = ad + db + ac + bc = 12 + 12 = 24 cм.
треугольник АСД прямоугольный, угол С=90°
найдем АД (гипотенуза) по теореме Пифагора
АД=√(3²+12²)=√(9+144)=√153
треугольник АВД прямоугольный, так как плоскости перпендикулярны. угол АДВ=90°, АД=√153, ВД=4, найдем АВ (гипотенуза) по теореме Пифагора
АВ=√((√153)²+4²)=√(153+16)=√169=13м
ответ АВ=13м