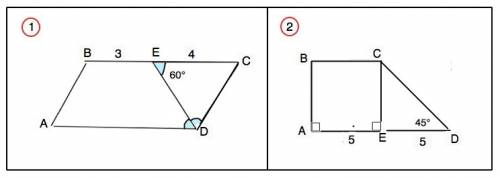
1) В параллелограмме противолежащие стороны равны и параллельны, противолежащие углы равны.
ДЕ - биссектриса, ⇒∠ЕDА=∠ЕDС.
∠СЕD=∠ЕDА – накрестлежащие. ⇒
треугольник СЕD равнобедренный, а так как углы при основании ЕD равны 60°, он - равносторонний.
Угол С=60°, угол А=угол С=60°. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°. ⇒∠В=∠D=120°
СD=ЕС=АС=4 см. АD=ВС=3+4=7 см
Р (АВСD)=2•(7+4)=22 см
Четырехугольник АВЕD - равнобедренная трапеция, так как ВЕ║|АD, и АВ=СД⇒АВ=ЕД.
-------------------
2) ∆ СЕD прямоугольный, Сумма острых углов прямоугольного треугольника 90°. ⇒
угол ЕСD=90°- 45*=45°⇒ ∆ СЕD – равнобедренный.
CE=ED=5
Перпендикуляр СЕ параллелен и равен АВ. -⇒
АВ=СЕ=5 см
Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
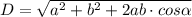
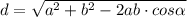
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол 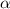
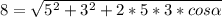
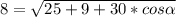
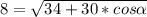
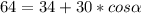
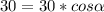
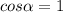

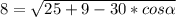

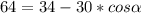
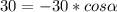
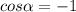
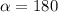
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.
sin a+cos a=√(5/3) или - √(5/3) Реализуются обе возможности:
первая - если a= (1/2)arcsin 2/3 (это я получил так:
умножил условие на 2, после чего удвоенное произведение синуса на косинус заменил на синус двойного угла),
вторая - если a=π+(1/2)arcsin 2/3 (в этом случае синус и косинус поменяют знак, произведение их при этом не изменится, а сумма изменит знак)