Прямые BD и m - скрещивающиеся прямые.
Объяснение:
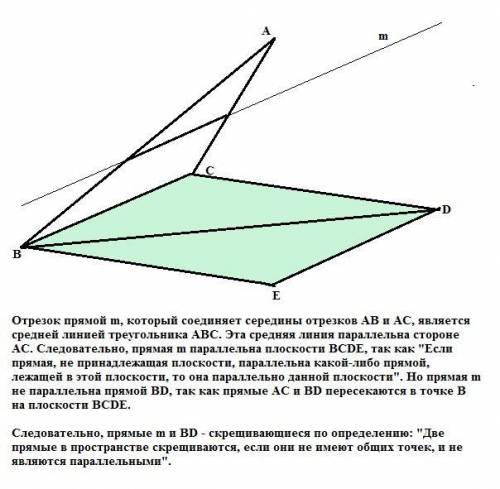
Отрезок прямой m, который соединяет середины отрезков AB и AC, является средней линией треугольника АВС. Эта средняя линия параллельна стороне АС. Следовательно, прямая m параллельна плоскости ВСDE, так как "Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости". Но прямая m не параллельна прямой BD, так как прямые АС и BD пересекаются в точке В на плоскости BCDE.
Следовательно, прямые m и BD - скрещивающиеся по определению: "Две прямые в пространстве скрещиваются, если они не имеют общих точек, и не являются параллельными".
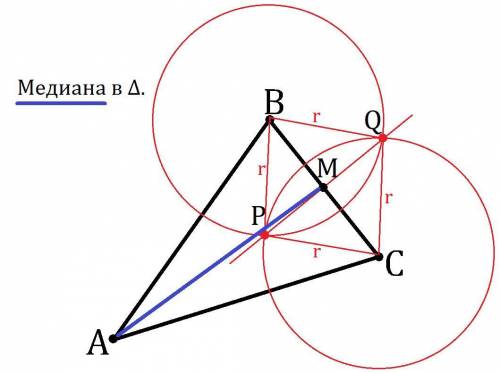
Медиана треугольника соединяет вершину треугольника и середину противоположной стороны, значит чтобы построить медиану нам нужно найти середину стороны. Пусть в ΔABC мы хотим провести медиану из вершины A на сторону BC, для этого:
Из точек B и C проводим с циркуля окружности с одинаковым радиусом r, при этом r зрительно больше половины BC (можно взять r = BC). Окружность пересекутся в двух точка Q и P, проводим с линейки прямую QP, QP∩BC = M, это и будет середина BC.
Это правда, потому что у четырёхугольника BQCP все стороны равны r, поэтому это ромб, а у ромба диагонали делятся точкой пересечения пополам.
Теперь с линейки соединяем точки A и M, полученные отрезок AM и будет медианой.
AC² = AB² + BC² - 2AB*BC*cosB
а) AC² = 8² + 5² - 2*8*5*0,5
AC² = 64 + 25 - 80 = 89 - 80 = 9
AC = √9
AC = 3
б) AC² = 7² + 3²- 2*7*3*0,5
AC² = 49 + 9 - 21 = 58 - 21 = 37
AC = √37
ответ: а)3; б)√37
2. Некорректное условие
3. S = ½ab*sinC
S = ½AC*BC*sinC
S=½*12*7*cos45=42*√2/2 = 21√2
ответ: 21√2