cos∠B = 0
cos∠A = 0,6
cos∠C = 0,8
Объяснение:
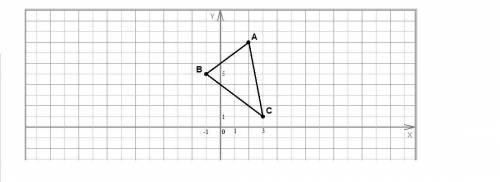
Найдем длины сторон треугольника по формуле расстояния между точками:
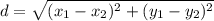
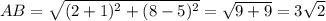
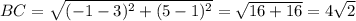

Проверим по теореме, обратной теореме Пифагора, не является ли этот треугольник прямоугольным:
AC² = AB² + BC²
(5√2)² = (3√2)² + (4√2)²
50 = 18 + 32
50 = 50 - равенство верно, значит треугольник прямоугольный с гипотенузой АС.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Косинус прямого угла равен нулю.
cos∠B = 0
cos∠A = AB / AC = 3√2 / 5√2 = 3/5 = 0,6
cos∠C = BC / AC = 4√2 / 5√2 = 4/5 = 0,8
∠ДВС=30°, ∠BДС=60°, значит Δ ВСД - прямоугольный.
АС и ВД пересекаются в точке Е. АЕ=СЕ=АС/2=6 см.
В прямоугольном тр-ке ВЕС СЕ лежит напротив угла в 30°, значит ВС=2СЕ=12 см.
В тр-ке ВЕД СД=СЕ/sin60=6·2/√3=4√3 см.
В тр-ке ВСД ВД²=ВС²+СД²=144+48=192,
ВД=8√3 см - это ответ.