
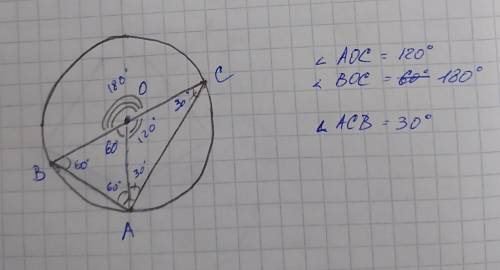
2. ∠AOC = 120°; ∠BOC = 180°; ∠ACB = 30°
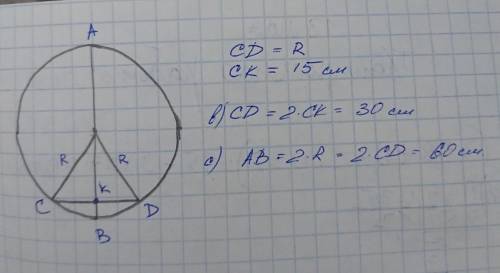
3. CD = 30 см; AB = 60 см
Объяснение:
2. Упростим соотношение дуг: 3:9:6 <=> 1:3:2 <=> AB, BC, AC
Найдём их градусную меру:
AB + BC + AC = x + 3x + 2x = 360°
6x = 360°
x = 60°
AB - 60°
BC - 180°
AC - 120°
Отразим это на рисунке.
Легко видеть, что
∠AOC = 120°; ∠BOC = 180°
На рисунке видно, что отрезок AO разделяет треугольник ABC на треугольник AOB и равнобедренный AOC. Поскольку сумма углов треугольника 180°, а угла у основания равнобедренного треугольика равны, то ∠ACB = (180° - 120°)/2 = 60°/2 = 30°
3. Рисунок и решение на фото.
См. объяснение
Объяснение:
1) Из точки А одним и тем же раствором циркуля делаем 2 засечки на прямой В. Визуально это получится как равнобедренный треугольник.
2) Из полученных засечек тем же раствором циркуля строим точку, симметричную точке А, но с другой стороны от прямой В. Назовём эту точку А1. Получилось, что мы таким образом построили два равных между собой равнобедренных треугольника с общим основанием. В получившемся четырёхугольнике все стороны равны (по построению), и противоположные углы попарно равны, - следовательно четырёхугольник является ромбом.
3) Диагонали ромба взаимно перпендикулярны.
Следовательно, если соединить А и А1 прямой, то мы таким образом построим диагональ ромба, которая перпендикулярна второй его диагонали, лежащей на прямой В, а значит, перпендикулярна и самой прямой В.