Отношение периметров подобных треугольников равно коэффициенту подобия
4,2 / (3+5+6) = 4,2 / 14 = 3/10= 0,3
стороны подобного треугольника:
3*0,3=0,9 (дм)
5*0,3=1,5 (дм)
6*0,3=1,8 (дм)
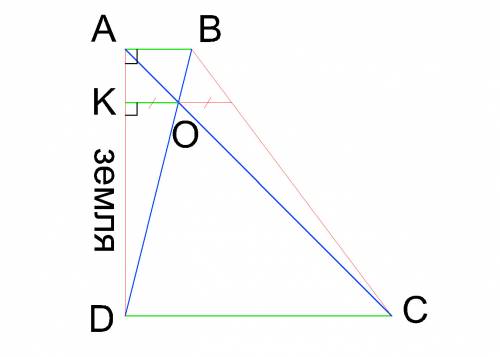
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Тогда рассмотрим треугольник, образованный пересечением диагонали, где одна диагональ перпендикулярна стороне.
Данный треугольник прямоугольный, один из его катетов равен 1/2•24 см = 12 см, а гипотенуза равна 1/2•26 см = 13, см.
Теперь по теореме Пифагора можно найти сторону параллелограмма:
√13² - 12² = √169 - 144 = √25 = 5 см.
Площадь параллелограмма равна произведению высоты на сторону. Тут высотой является диагональ, равная 24 см.
Тогда площадь параллелограмма равна:
S = 24 см• 5 см = 120 см²
ответ: 120 см².