Длина диаметра - это всего лишь высота данной трапеции, если из вершины тупого угла провести высоту, то ее легко найти из прямоугольного треугольника с боковой стороной, равной 180/4=45(т.к. сумма оснований трапеции должна равняться сумме боковых сторон, т.е. равна 90см, иначе не опишешь трапецию, а т.к. трапеция равнобедренная, то боковые стороны равны по 90/2=45/см/)
...так вот.. отвлекся
Чтобы найти высоту, т.е. катет, лежащий против угла в 30°, надо гипотенузу /т.е. боковую сторону трапеции/ разделить надвое, 45/2=22,5/см/
ответ 22,5 см
DE = 24 см
Объяснение:
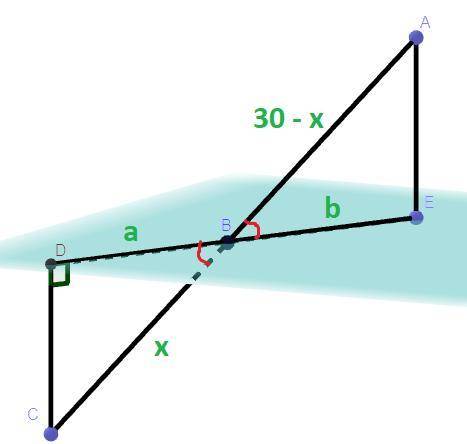
Дано: АС = 30 см, DC = 6 см, AE = 12 см, DC ⊥ ED, AE ⊥ DE
Найти: DE - ?
Решение: Пусть BD = a, BE = b. СB + AB = AC ⇒ AB = AC - BC = 30 - BC.
Пусть BC = x, тогда AB = 30 - x. Треугольник ΔCBD подобен ΔBAE по двум углам так как по условию DC ⊥ ED, AE ⊥ DE, то ∠CDB = ∠AEB = 90°, а углы ∠DBC = ∠ABE как вертикальные углы, из подобия треугольника ΔCBD треугольнику ΔBAE следует, что
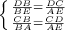
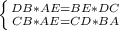
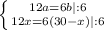
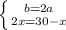
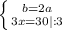
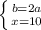
Рассмотрим треугольник ΔCDB. BD = x = 10 см. По теореме Пифагора:
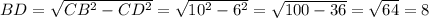 см.
см.
b = 2a ⇔ BE = 2BD = 2 * 8 = 16 см.
DE = BE + BD = 16 + 8 = 24 см.