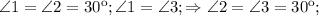 )
) 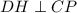 ,
, 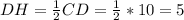 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD.  ,
, 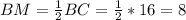 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 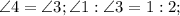
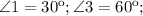 Тогда в ромбе
Тогда в ромбе 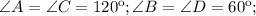
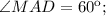 , тогда
, тогда 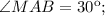 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 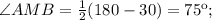
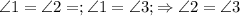 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 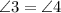 ,
, 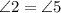 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.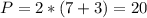 .
.
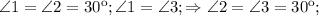 )
) 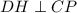 ,
, 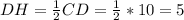 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 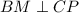 ,
, 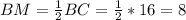 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 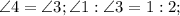
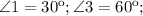 Тогда в ромбе
Тогда в ромбе 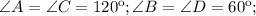
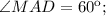 , тогда
, тогда 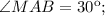 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 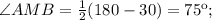
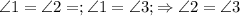 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 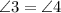 ,
, 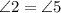 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.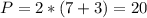 .
.
В основании правильной четырёхугольной пирамиды лежит квадрат, сечение, параллельное основанию пирамиды, очевидно, также является квадратом. В условии данной задачи даны, можно сказать, две таких пирамиды, бОльшая и мЕньшая, и есть соотношения высот и площадей оснований, это прежде всего связано с объемом пирамиды, составляем соотношения. V₁ , V₂ - объём первой и второй пирамид.
V₁ / V₂ = (1/3)•S₁•h₁ / (1/3)•S₂•h₂ = S₁•h₁ / S₂•h₂
Очевидно, пирамиды подобны, и отношение их объёмов равно кубу коэффициента подобия
S₁•h₁ / S₂•h₂ = k³
27•3x / S₂•7x = (3/7)³ = 27/343 ⇒ S₂ = 343•3/7 = 147
ответ: 147