расстояние от K до ABC (обозначим KO) - это перпендикуляр к ABC => из прямоугольного треугольника KOA по т.Пифагора KO = корень(AK^2-AO^2). AK=10 по условию.
Точка O - центр треугольника ABC, она лежит на высоте(медиане и биссектрисе) AN и делит AN в отношении 2:1 AO=2*ON
из прямоугольного треугольника ABN AN = корень(AB^2-BN^2). AB=15 по условию, BN=15/2 (т.к. AN высота и медиана правильного треугольника) AN = корень(15*15-15*15/4) = корень(3*15*15/4) = 15/2*корень(3)
ON = AN/3 = 5/2*корень(3)
AO = 2*ON = 5*корень(3)
KO = корень(10*10-5*5*3) = корень(100-75) = корень(25) = 5
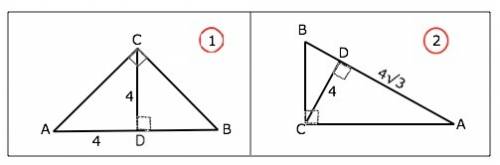
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°