Равносильно - найти сторону равностороннего треугольника, если радиус описанной окружности 35*корень(3).
Такое хитромудрое решение :))) радиус ВПИСАННОЙ окружности = 35*корень(3)/2,
половина стороны равна (35*корень(3)/2)*корень(3) = 105/2, сторона 105 :)))
На самом деле я воспользовался кучей особенностей равносторонего треугольника, а можно сразу записать по теореме синусов a = 2*R*sin(60) = 105.
Можно сказать, что высота равна (3/2)*R (опять используется совпадение центров), а сторона равна h/(корень(3)/2); ответ будет одинаковый.
а = 105.
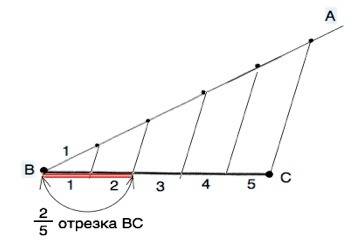
Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
Также, если угол в прямоугольном треугольнике равен 60 гр,то второй угол будет равен 30 гр (90-60=30), а противолежащий катет угла 30 градусов равен половине гипотенузы.
Из этого следует, что треугольник ABC прямоугольный.
Биссектриса BD образовала новый прямоугольный треугольник ABD.
AB=a
BD=?
угол ABD=30 градусов
Найдём BD через косинус ABD (косинус угла в 30 градусов можно найти в таблице синусов и косинусов).
См. картинку