В задании на рисунке две прямых с.
Изменив рисунок, получаем: прямая d пересекает три прямые a, b и с.
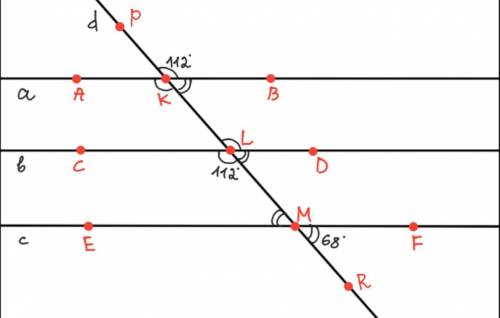
Чтобы была возможность именовать углы, обозначим на прямых точки A, B, C, D, E, F, K, L, М, Р и R (см. рисунок).
Не забываем: )
Если при пересечении двух прямых секущей накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые параллельны.
1) Вертикальные углы при пересечении двух прямых всегда равны, а это значит:
∠РКВ=∠AKL=112°,
∠KLD=∠CLM=112°,
∠EML=∠RMF=68°.
2) Как видим из предыдущего пункта, ∠PKB=∠KLD=112° ⇒ прямые a и b параллельны, т.к. углы равны как соответственные, а прямая d — секущая.
3) Прямые b и c тоже параллельны, покажем это.
Известно, что ∠CLM=122°, ∠EML= 68°.
∠CLM+∠EML=122°+68°=180°.
Согласно теореме, если две прямые при пересечении секущей параллельны, то их односторонние углы в сумме составляют 180°.
∠CLM+∠EML=180° ⇒ прямые b и c параллельны! (т.к. сумма одностор. углов 180°, прямая d — секущая)
4) Из 2 и 3 пунктов известно, a||b и b||c ⇒ a||c ⇒ a||b||c.
ответ: прямые а, b и с параллельны.
-1x -1y +1 =0 или y = 1-x.
Объяснение:
Найдем уравнение прямой, проходящей через две точки по формуле:
(X - Xm)/(Xn-Xm) = (Y-Ym)/(Yn-Ym). Тогда
(X - (-1))/(0-(-1)) = (Y-2)/(1-2). =>
(X+1)/1 = (Y-2)/-1 =>
-1x -1y +1 =0 или y = 1 - x.
Второй вариант:
Уравнение прямой можно записать так:
y = kx + b.
Точки М(-1;2) и N(0;1) лежат на этой прямой. значит координаты этих точек должны удовлетворять уравнению прямой.
Подставим координаты точек в уравнение и получим:
2 = k·(-1) + b. (1)
1 = k·(0) + b. (2) Из (2) получаем значение: b =1.
Подставим b в (1) и получим k = -1.
Тогда наше уравнение примет вид:
y = -x + 1 или
-1x - 1y + 1 = 0.
так как СД=ДЕ, то треугольник СДЕ - равнобедренный, значит угол С= углу Е = 51 градусов, так как 180-78= 102 и 102/2= 51 градус угол С и угол Е
по теореме синусов:
16 СД
=
син78 градусов син 51 градуса
по таблице брадиса находим синусы и получается,
СД = (16*0,7771)/0,9781≈12,71