Цитаты: "Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). Линейный угол - это угол, образованный пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней.
АВ- двугранный угол, точка М удалена от плоскостей на расстояние m, то есть МС=МD=m. DК и CK перпендикулярны AB (теорема о трех перпендикулярах). <DKC- линейный угол данного нам двугранного угла, равного 120*. Проведем МК. Поскольку точка М равноудалена от сторон угла DKC, МК - биссектриса этого угла и <МКС=120° /2=60°.
В прямоугольном треугольнике КМС <MKC=60*, значит <KМC=30°. Следовательно КМ=2КС и по Пифагору 4КС²-КС²=m². Тогда КС=m/√3.
Поскольку МК=2КС , МК=2m/√3 или МК=2m√3/3.
Объяснение:
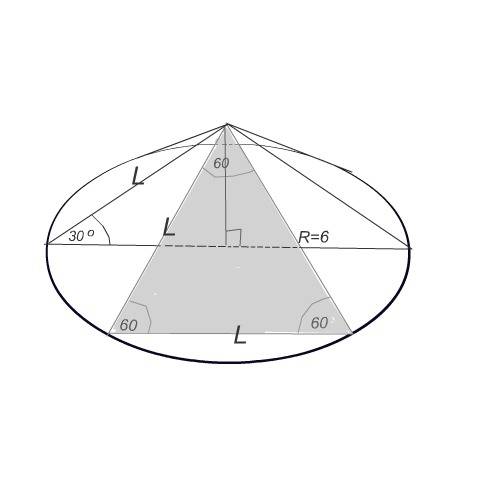
Образующая конуса наклонена к плоскости основания под углом 30°.
Плоскость сечения образована сторонами, равными образующей, и угол между ними 60°
Плоскость сечения - правильный треугольник.
Треугольник, образованный образующей, радиусом конуса и его высотой - половина правильного треугольника.
Высота - катет этого треугольника и равна половине образующей.
Второй катет равен радиусу основания и, как высота правильного треугольника
( можно и по теореме ПИфагора найти), равен (а√3):2=(L√3):2
(L√3):2=6
L√3=12 см
L=12:√3=12√3:√3*√3=12√3:3=4√3 см
Как уже сказано, плоскость сечения - равносторонний треугольник.
Формула площади равностороннего треугольника
S=(a²√3):4
S=(L√3)²√3:4=S=(16 *3)√3:4=48√3:4
S= 12√3 cм²