Объяснение:
. а) Сумма внутренних углов треугольника равна 180°. Значит третий угол треугольника равен 180°-70°--55°=55°. В треугольнике два угла равны, значит треугольник равнобедренный с основанием ВС, так как равные углы прилежат к стороне ВС.
б) Так как ВМ -перпендикуляр к АС, то треугольники АВМ и СВМ - прямоугольные. Сумма острых углов прямоугольного треугольника равна 90°, значит <АВМ=90°-70°=20°. <СВМ=90°-55°=35°.
2. а) Треугольники ВСО и ВСD равны по двум сторонам и углу между ними (АО=ОВ и СО=OD - дано, а <АОС =<BOD - вертикальные).
Что и требовалось доказать.
б) В равных треугольниках против равных сторон лежат равные углы. Следовательно, <ОАС=<OBD. Угол OBD=180°-20°-115°=45°.
ответ: <ОАС=45°.
Подробнее - на -
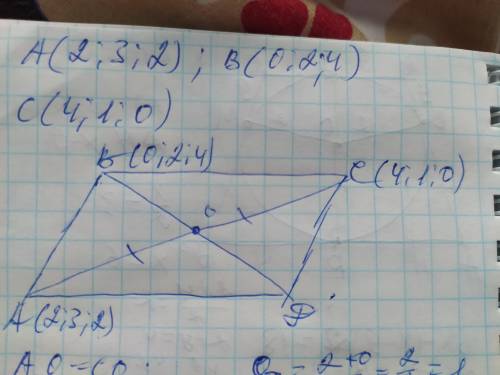
ответ: Д(6; 2; -1)
Объяснение: найдём координаты точки О - середины диагонали АС по формуле: Ох=(Ах+Сх)/2; Оу=(Ау+Су)/2;
Oz=(Аz+Cz)/2. Подставим данные координаты а формулу:
Ox=(2+4)/2=6÷2=3
Оу=(3+1)/2=4÷2=2
Оz=(2+0)/2=2/2=1
Итак: координаты О(3; 2; 1)
Так как координаты середины диагонали АС совпадает с серединой диагонали ВД, то:
Ох=(Ах+Дх)/2. Оу=(Ву+Ду)/2
3=(0+Дх)/2. 2=(2+Ду)/2
Дх=3×2. 2+Ду=2×2
Дх=6. Ду=4-2
Ду=2
Oz=(Bz+Дz)/2
1=(4+Дz)/2
4+Дz=2×1
Дz=3-4
Дz= -1
Координаты Д(6; 2; -1)
r(цил.)=2 см
h(цил.)=2 см
Найти: Vпар.=? см³
Решение
Vпар.=Sосн.*h
В основании параллелепипеда лежит квадрат, сторона которого больше радиуса вписанной в него окружности в 2 раза (2r=d (диаметр)) и равна: 2*2=4 см.
Sосн.=4²=16 см.
Высота параллелепипеда является равной высоте цилиндра: hпар.=hцил.=2 см.
Vпар.=Sосн.*h=16*2=32 (см³)
ответ: объём параллелепипеда равен 32 см³