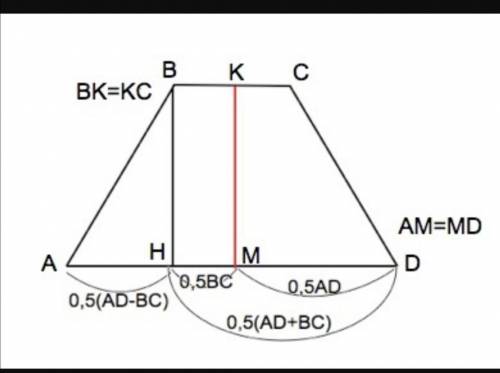
Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на отрезки, один из которых равен полусумме оснований, другой - их полуразности.
1) (15+9):2=12 см
2)(15-9):2=3 см
----------
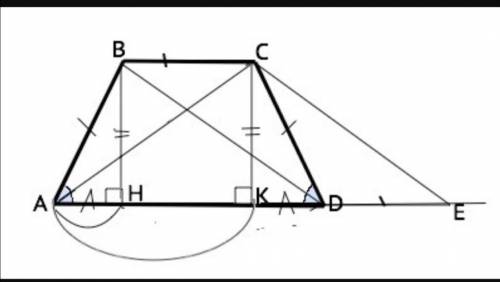
Действительно, треугольники, которые отсекают две высоты равнобедренной трапеции, равны (см. рисунок).
Отсюда АН=(АD-BC):2
Проведем из С прямую параллельно диагонали , ВD до пересечения с продолжением АD в точке Е. DE║BC⇒CEDВ параллелограмм, DE=BC
АЕ=АD+BC
Треугольник АСЕ равнобедренный, его высота СК - медиана⇒
АК=АЕ:2, как и НD=АК=( АD+BC):2
----------
Рисунок второго приложения проще и не нуждается в особых комментариях.
Объяснение:
первыфй угол-1х
второй-2х
третий-3х
сумма углов тркугольника-180, значит
\х+2х+3х=180
6х=180
х=180:6
х=30
первый угол- 30°
второй-2*30=60°
третий-3*30=90°