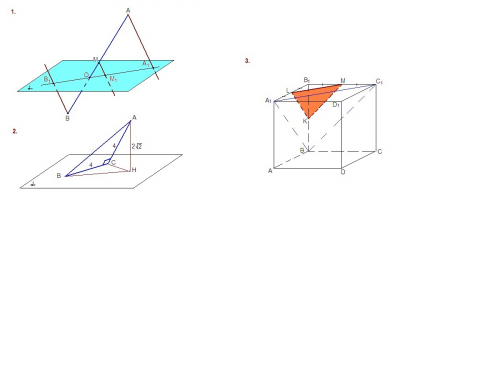
1) Секущая плоскость пересекает параллельные грани по параллельным прямым. Она пересекает грань ВВ₁С₁С по прямой ВС. Так как точка А₁ принадлежит сечению, то секущая плоскость пересекает грань АА₁D₁D по прямой A₁D₁ (BC║A₁D₁).
A₁D₁CB - искомое сечение.
Расположение точки М не дано. Возьмем точку на ребре АА₁.
По признаку параллельности плоскостей, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
Проведем в грани АА₁В₁В отрезок MF║А₁В, в грани AA₁D₁D отрезок МЕ║A₁D₁.
Плоскость грани АВСD пересекает параллельные плоскости (желтую и голубую) по параллельным прямым, поэтому в грани АВСD проводим отрезок FK║BC. Соединяем точки Е и К.
MEKF - искомое сечение.
2) В задании пунктов а) и в) точка М расположена одинаково. В пункте а) не сказано, как проходит сечение, а через одну точку можно провести бесконечно много сечений. Поэтому эти пункты объединим, стоим сечение тетраэдра плоскостью, проходящей через точку М, параллельно прямым АС и BD.
а) и в) Проведем в грани ACD МК║АС, а в грани BCD МР║BD.
МР║BD, а значит и плоскости ABD. Сечение проходит через МР и пересекает ABD, значит линия пересечения параллельна BD. Проводим КЕ║BD.
МК║АС, а значит и плоскости АВС. Сечение проходит через МК и пересекает АВС, значит линия пересечения параллельна АС. Значит получилось, что ЕР║АС.
МКЕР - искомое сечение. Имеет вид параллелограмма, так как противоположные стороны параллельны (МК и РЕ параллельны АС, значит МК║РЕ, КЕ и МР параллельны BD, значит КЕ║МР).
Сечение может быть ромбом, если речь идет о правильном тетраэдре и точка М будет серединой стороны CD. Тогда все стороны сечения будут средними линиями граней тетраэдра и будут равны.
б) Соединим точки, находящиеся в одной грани: М и N, N и К.
Прямая MN лежит в грани BCD, эта грань пересекает плоскость грани ABD по прямой BD. Продлим MN до пересечения с прямой BD (точка Р).
Теперь точки Р и К лежат в плоскости одной грани ABD; проводим прямую РК. Она пересечет ребро AD в точке Т.
Соединяем М и Т.
МNKT - искомое сечение.

Если биссектриса острого угла трапеции является его диагональю, то меньшее основание трапеции равно её боковой стороне.
Имеем АВ = ВС =СД = а.
Опустим перпендикуляр СЕ из точки С на АД.
При этом получили 2 подобных треугольника: АСЕ и ЕСД.
Угол САЕ равен углу ДСЕ как взаимно перпендикулярные.
Угол А равен углу Д (как углы при основании равнобедренной трапеции).
Поэтому угол ДСЕ равен половине угла Д.
Имеем: 90° =(1/2)Д+Д = (3/2)Д,
Отсюда угол Д = 90*2/3 = 180/3 = 60°.
Тогда ЕД = а/2, а основание АД = а+2(а/2) = 2а.
Высота СЕ = а*sin 60° = a√3/2.
Площадь S трапеции равна:
S = ((a+2a)/2)*(a√3/2) = (3a/2)*(a√3/2) = 3√3a²/4.
То есть данная трапеция равна площади трёх равносторонних треугольников со стороной а.