1. Известно, что треугольник с искомыми сторонами подобен исходному, то есть все соответственные элементы у треугольников соотносятся как коэффициент подобия.
Пусть коэффициент подобия равен 
. Тогда стороны второго треугольника равны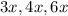 
. А их сумма, то есть периметр, рана 58,5 см.
Имеем уравнение
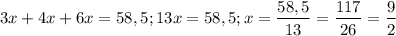
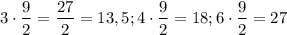
ответ: 13,5 см, 18 см, 27 см.
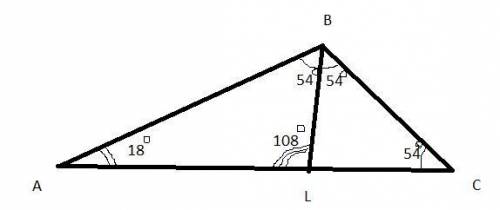
2. Сумма углов треугольника равна 180°. Третий угол равен 180°-(54°+18°)=108°
Далее, биссектриса делит угол пополам, то тупой угол будет разбит на два угла по 108°/2=54°
Получится два треугольника (рисунок приложен)
Рассмотрим треугольник, в котором присутствует угол 18° из исходного треугольника (левый на рисунке). Второй угол равен 54°. Но и в исходном треугольнике есть углы 18° и 54°, а это означает, что этот отсеченный треугольник подобен исходному треугольнику (по двум углам). Второй отсеченный треугольник, кстати, является равнобедренным (имеет два угла по 54°).
В правильном треугольнике высоты, как и медианы, в точке пересечения делятся в отношении 2:1, считая от вершины.
Найдем по Пифагору ОН из треугольника SOH: ОН=√(SH²-SO²) или ОН=√(8²-4²)=4√3.
Это 1/3 высоты треугольника.
Значит высота треугольника - основания равна 12√3.
Сторону правильного треугольника найдем из формулы для высоты: h= √3*a/2, то есть а=2h/√3=24√3/√3=24.
Площадь основания равна: S=√3*a²/4 или
S=√3*576/4=144√3.
Объем пирамиды равен V=(1/3)*S*H или
V=(1/3)*144√3*4=192√3 см².
ответ: V=192√3 см².