S = 50 ед².
Объяснение:
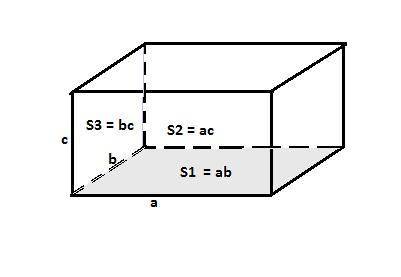
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².
Объяснение:
Определение
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Теорема 1
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Доказательство:
Пусть а прямая, перпендикулярная прямым b и c в плоскости . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости .
Проведем произвольную прямую х через точку А в плоскости и покажем, что она перпендикулярна прямой а. Проведем в плоскости произвольную прямую, не проходящую через точку А и пересекающую прямые b, c и х. Пусть точками пересечения будут В, С и Х.
Отложим на прямой а от точки А в разные стороны равные отрезки АА1 и АА2. Треугольник А1СА2 равнобедренный, так как отрезок АС является высотой по условию теоремы и медианой по построению (АА1=АА2). по той же причине треугольник А1ВА2 тоже равнобедренный. Следовательно, треугольники А1ВС и А2ВС равны по трем сторонам.
Из равенства треугольников А1ВС и А2ВС следует равенство углов А1ВХ и А2ВХ и, следовательно равенство треугольников А1ВХ и А2ВХ по двум сторонам и углу между ними. Из равенства сторон А1Х и А2Х этих треугольников заключаем, что треугольник А1ХА2 равнобедренный. Поэтому его медиана ХА является также высотой. А это и значит, что прямая х перпендикулярна а. По определению прямая а перпендикулярна плоскости . Теорема доказана.