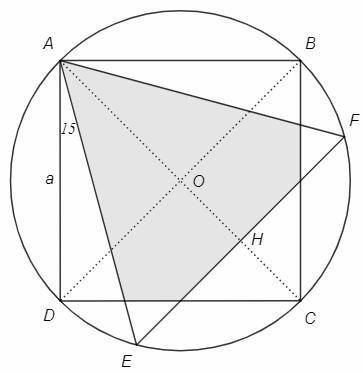
От квадрата со стороной a отсечены:
треугольник, равный 1/8 площади квадрата
два симметричных треугольника с катетами a и a*tg15
Искомая площадь равна
S= a^2(1 -1/8 -tg15) =a^2(8√3 -9)/8
R - радиус описанной окружности
Сторона квадрата a =R√2
Сторона треугольника 12 =R√3
a= 12*√2/√3 =4√6
S= 12(8√3 -9) =96√3 -108
Центр окружности - на пересечении диагоналей квадрата. Треугольник имеет с квадратом общую вершину, следовательно серединный перпендикуляр к основанию совпадает с диагональю квадрата.
AO/OH =2/1 (AH - медиана), AO=OC (радиусы) => OC/OH =2/1.
BD⊥AC, EF⊥AC => BD||EF. По теореме Фалеса EF делит стороны BC и CD в том же отношении, что и OC, то есть пополам.
DAE= (DAB-EAF)/2 =(90-60)/2 =15
tg15 =tg(30/2) =(1-cos30)/sin30 =2(1-√3/2) =2-√3
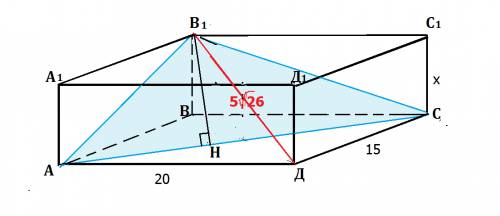
Пусть Н - искомое расстояние от точки до прямой
По теореме Пифагора: х² + Н² = 10² и (16 - х)² + Н² = 18²
Вычтем из второго равенства первое
(16 - х)² - х² = 18² - 10²
256 - 32х + х² - х² = 324 - 100
-32х = 224 - 256
32х = 32
х = 1
Из равенства х² + Н² = 10² найдём Н
Н = √ 100 - 1 = √99 ≈ 9,95