Расстояние от точки до сторон квадрата равно 13 см. Найдите расстояние от точки до плоскости квадрата, если сторона квадрата равна 10 см. можете объяснить, с рисунком
Объяснение:
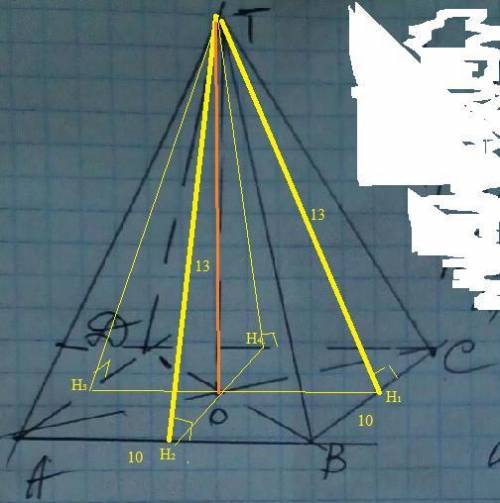
Расстояние от точки Т до плоскости отрезок ТО ⊥ ( АВС) . Значит ТО перпендикулярен любой прямой лежащей в плоскости.
Т.к. расстояние -это перпендикуляр, то опустим перпендикуляры из точки Т на стороны квадрата : ТН₁ , ТН₂ , ТН₃ , ТН₄. Тогда прямоугольные треугольники ( на рисунке желтые) равны по катету и гипотенузе ( апофема боковой грани).⇒точка О -центр вписанной окружности и еще т. пересечения диагоналей квадрата.
Н₁ Н₃= 10 , ОН₁=5 , из ΔТОН₁ , по т. Пифагора ТО=√(13³-5²)=√144=12 (см)
Фалес Милетский – древнегреческий философ, родоначальник античной и вообще европейской философии и науки, основатель милетской школы. Сочинения Фалеса не сохранились, однако Аристотель называет его первым ионийским философом.
Происходил из г. Милета (Малая Азия). По преданию, много путешествовал по странам Востока, учился у египетских жрецов и вавилонских халдеев. Используя полученные в Египте знания, Фалес предсказал солнечное затмение 28 мая 585 г. до н. э., которое лидийскому царю Алиатту принудить мидян к миру на выгодных условиях. Во время войны с персами Фалес проектировал инженерные сооружения для армии другого лидийского царя – Креза.
В своей натурфилософии Фалес возводил всё многообразие явлений и вещей к единой основе (первостихии или первоначалу), которой считал «влажную природу», воду: всё возникает из воды и в неё превращается.
Вселенная, по представлению Фалеса, представляет жидкую массу, посередине которой находится воздушное тело, имеющее форму чаши, повёрнутой открытой стороной вниз. Вогнутая поверхность этой чаши – небо; на нижней поверхности, в центре её, плавает диск, обтекаемый водой. Звёзды – боги, плавающие по небесному своду.
Для философии Фалеса характерен гилозоизм: «мир одушевлён и полон богов»: вслед за Гомером он представлял душу в виде тонкого (эфирного) вещества.
S=mh=92 h=8 ⇒ m=11,5
Средняя линия трапеции m равна полусумме двух оснований трапеции .
Получаем систему: