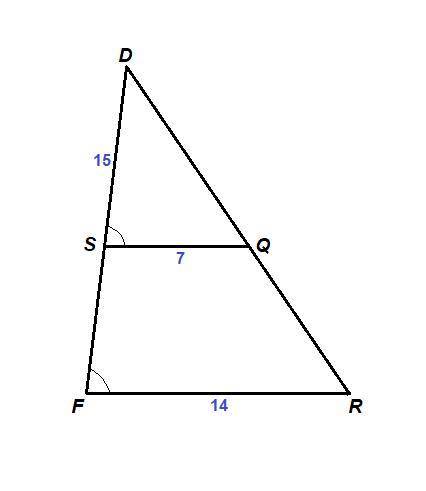
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.
4√37 см
Объяснение:
∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит
ΔDSQ ~ ΔDFR по двум углам.
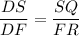
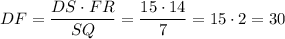 см
см
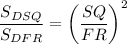
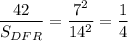
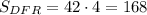 см²
см²
Площадь треугольника DFR можно вычислить так же по формуле:
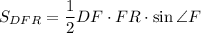
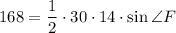
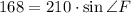
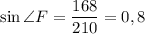
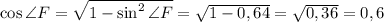
Из треугольника DFR по теореме косинусов:
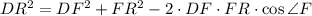
DR² = 30² + 14² - 2 · 30 · 14 · 0,6
DR² = 900 + 196 - 504 = 592
DR = √592 = 4√37 см
Основанием пирамиды является равнобедренный треугольник с углом α при основании и радиусом вписанной окружности г. Две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания, а третья - наклонена к ней под углом β. Найдите объём пирамиды.
Объяснение: V(пир.)=1/3*S(основания)*h , h- высота пирамиды.
1) Найдем S(основания)=S(ΔАВС)=1/2*АС*ВН=АН*ВН.
Из ΔАВН ,угол ∠АВН=90°-α. По свойству касательной ОР⊥АВ, ОР=r ,Тогда из ΔВРО-прямоугольного 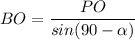 или
или 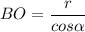 .
.
Высота ВН=ВО+ОН , 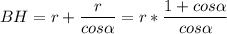 .
.
Из ΔАОН ,найдем АН. Тк АО-биссектриса , то ∠ОАН=α/2 ⇒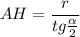 .
.
S(ΔАВС)=АН*ВН=  .
.
2) Т.к две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания , то линия пересечения , отрезок МВ⊥(АВС)⇒ МВ-высота пирамиды..
Т.к ВН⊥АС , то и наклонная МН⊥АС по т. о трех перпендикулярах.Тогда углом между плоскостями (АВС) и ((АМС) будет линейный угол ∠ВНМ=β.
ΔМВН-прямоугольный , ,
,
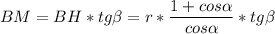 ,
, 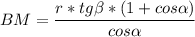 .
.
3)Обьем 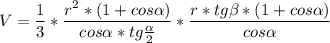 ,
,
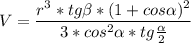 .
.

т.е. тр. АВС - равнобедренный
АС=ВС=7 см
Далее по теореме Пифагора
АВ²=АС²+ВС²
АВ²=49+49
АВ=7√2
ответ: 7√2