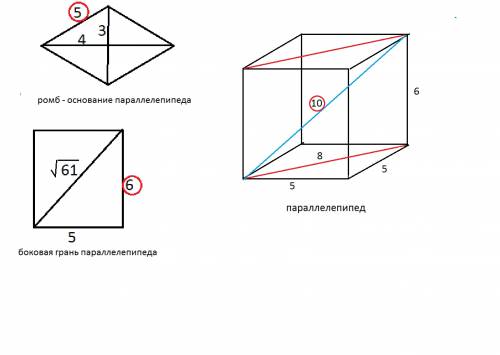
1) По теореме Пифагора ( или приняв во внимание, что половины диагоналей и сторона ромба составляют египетский треугольник) из прямоугольного треугольника=1/4 ромба найдем его сторону.
Она равна 5 см (√(3²+4²)
2)Из боковой грани найдем высоту параллелепипеда.
Она равна 6 см (√(61-5²)
3) Из прямоугольника, сторонам которого равны два ребра и две диагонали оснований параллелепипеда ( 6,6,8,8) находим большую диагональ параллелепипеда.
она равна 10 см. (√(6²+8²)
4)Площадь полной поверхности параллелепипеда = 2 Sосн + S бок
Sосн=S ромба=d·D:2=6·8:2=24 см²
S бок=Р·Н=5·4·6=120 см²
Sполн=120+2·24=168 см²
AO =OB =AB/2 ;
CO =OD =CD/2.
--------------------------------------
Док- ать AO < (AC + AD) /2
Концы отрезков являются вершинами параллелограмма.
( Соединяем точки (концы отрезков) A и С , A и D , B и С , B и D ).
Действительно :
ΔAOC = ΔBOD ( по первому признаку равенства треугольников)
следовательно AC = BD и ∠OAC =∠OBD , но эти углы накрест лежащие , поэтому AC | | DB . И наконец из AC = BD и AC | | DB следует (⇒)
четырехугольник AСBD является параллелограммом.
Из ΔADB :
AB < AD + DB ( неравенство треугольника) ;
2AO < AD +AC ;
AO < ( AC+AD) / 2 . * * * что и требовалось доказать * * *
см рисунок (приложения