7,3
Объяснение:
Большее основание - 9,5 (нижнее)
Меньшее - 2,2 (верхнее)
Один из углов - 45 (этот угол находится между нижнем основанием и большей боковой стороной)
Меньшая боковая сторона - сторона при прямом угле трапеции.
Проведём высоту так, чтобы получить прямоугольный треугольник с углом в 45 (при основании трапеции), которая будет равна меньшей боковой стороне (так как основания трапеции параллельны, а высота - перпендикулярна к обоим основаниям). Если один угол 45 в прямоугольном треугольнике, то и второй тоже 45. Треугольник равнобедренный, значит его катеты равны. Найдем катет лежащий на нижнем основании (9,5-2,2) = 7,3. Второй катет равен тоже 7,3 так как треугольник равнобедренный. Этот второй катет и будет высотой трапеции, которая равна меньшей боковой стороне.
1), 2), 6), 8).
Объяснение:
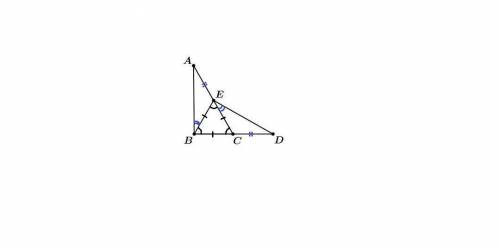
ΔАВС = ΔDEB,
АВ = DE, АС = DB, значит ВС = ВЕ, т.е. ΔВЕС равнобедренный
В равных треугольниках против равных сторон лежат равные углы, значит
∠DBE = ∠ACB, тогда
ΔВЕС равнобедренный с основанием ВС.
Итак, ВЕ = ЕС = ВС, т.е. ΔВЕС равносторонний.
∠АВЕ = ∠АВС - ∠ЕВС
∠DEC = ∠DEB - ∠BEC
∠АВС = ∠DEB из равенства треугольников,
∠EBC = ∠BEC, как углы равностороннего треугольника, значит
∠АВЕ = ∠DEC.
АЕ = АС - ЕС
CD = DB - BC
AC = DB по условию,
ЕС = ВС, так как ΔВЕС равносторонний, значит
АЕ = CD.
1) Треугольник BCE равнобедренный - верно.
2) Треугольник BCE равносторонний - верно.
3) ∠ABC = 90° - нельзя утверждать.
4) Треугольник ECD равнобедренный - нельзя утверждать.
5) AE = BC - нельзя утверждать.
6) AE = CD - верно.
7) ∠ABE = ∠CDE - нельзя утверждать.
8) ∠ABE = ∠CED - верно.