ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
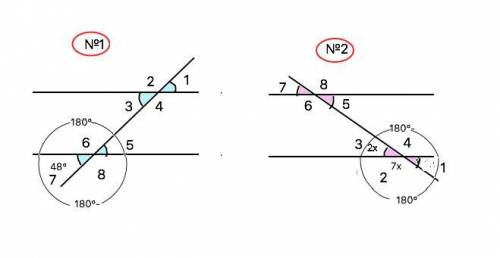
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Значится рисуем тупоугольный треугольник abc, в котором тупой угол c, а сторона ac=bc и ∠a=∠b
Из вершины b проводим высоту к продолженной стороне ac, т.е. высота лежит за пределами Δabc, точку пересечения с продолженной стороной обзовем k, получим высоту bk
Теперь проведём биссектрису из вершины b к стороне ac, в точке пересечения поставим f.
Получим угол между биссектрисой и высотой, т.е. ∠fbk=48°
Примем ∠fbc=x, тогда ∠a=∠b=2x
Чтобы найти ∠с нужно сначала найти ∠f, рассмотрим Δfbk:
Сумма трёх углов =180°, значит ∠f=180-90-48=42°
Теперь рассмотрим Δfbc и выразим ∠c:
∠c=180-42-x
∠c=138-x
Теперь возвращаемся к нашему исходному Δabc и составляем уравнение:
2х+2х+(138-х)=180
4х+138-х=180
3х=42
х=14
∠a=∠b=2x
Подставляем, получаем
∠a=∠b=28°
∠c=180-28-28
∠c=124
ответ: углы треугольника равны 28, 28 и 124 градуса