y = 2sinx + 1
Объяснение:
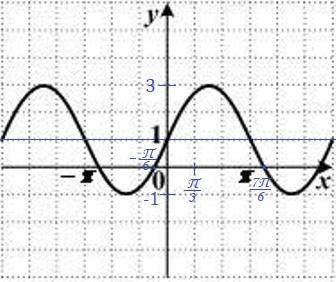
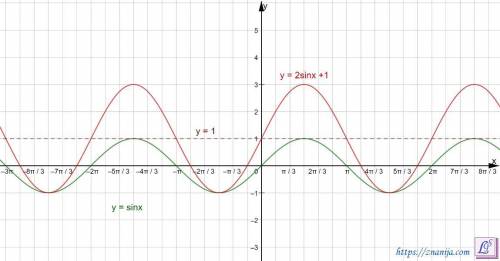
На рисунке изображен график функции y = 2sinx + 1
График функции y = sinx сдвинут относительно оси Y на +1 единицу, коэффициент растяжения вдоль оси Y = 2.
Свойства функции y = 2sinx + 1.
Функция y = 2sinx + 1 периодическая, период T = 2π
Ось Y пересечена в т.(0; 1 ):
x = 0; y = 2*sin0 + 1 = 2 * 0 + 1 = 1
Нули функции:
y = 0; 2sinx+1 = 0; sinx = -1/2
x₁ = arcsin(-1/2) + 2πn = 7π/6 + 2πn; n∈Z
x₂ = π - arcsin(-1/2) + 2πn = π - 7π/6 + 2πn = -π/6 + 2πn; n∈Z
Максимальное значение функции y = 2 * 1 + 1 = 3 (т.к. максимальное значение функции sinx = 1)
Минимальное значение функции y = 2 *(-1) + 1 = -2 + 1 = -1 (т.к. минимальное значение функции sinx = -1).
Объяснение:
1. Задание
Сумма двух сторон треугольника должна быть больше третьей стороны.
а) 5+5=10; 10>5, да такой треугольник существует называется правильный треугольник.
б)5+8=13; 13>9
5+9=14; 14>8
8+9=17; 17>5
Да такой треугольник существует.
в)
8+9=17; 17<45 нет такой треугольник не существует.
2. Задание
1+1+2=4 коэффициент.
Сумма углов в треугольнике равна 180°
180°:4=45
45*1=45° градусная мера одного угла
45*1=45° градусная мера второго угла
45*2=90° градусная мера третьего угла.
Или решение уравнением.
Пусть градусная мера одного угла будет <1=х, тогда градусная мера второго угла будет <2=х, а градусная мера третьего угла <3=2х. Составляем уравнение
х+х+2х=180°
4х=180°
х=180°:4
х=45° градусная мера первого и второго угла.
Градусная мера третьего угла равна 2х, подставляем значение х.
2*45°=90°
ответ: градусная мера углов в треугольнике равна <D=45°;<E=45°;<P=90°
3. Задание.
Треугольник равнобедренный.
Пусть основание треугольника будет х, тогда боковая сторона будет х+30(так как треугольник равнобедренный то таких сторон две.) Составляем уравнение
х+2(х+30)=330
х+2х+60=330
3х=330-60
3х=270
х=270:3
х=90 см. Основание треугольника (АВ).
Боковая сторона (СВ=АС) равно
х+30, подставляем значение х.
90+30=120 см. боковая сторона треугольника.
ответ : АВ=90см; СВ=120см; АС=120см.
Проверка
90+120+120=330 (периметр треугольника)
∠AOD и ∠DOB - смежные; сумма смежных углов равна 180°;
∠AOD = 180°-∠DOB = 180°-64° = 116°.
Биссектриса делит угол пополам, OK - биссектриса ∠AOD;
∠AOK = ∠AOD:2 = 116°:2 = 58°.
ответ: 58.