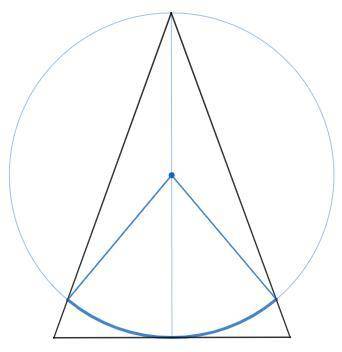
Угол при основании равнобедренного треугольника равен 70°. На высоте треугольника, проведенной к основанию и равной 27 см, как на диаметре построена окружность. Найдите длину дуги окружности, которая принадлежит треугольнику.
Длина окружности диаметром d равна пd
Длина дуги ф градусов равна пd *ф/360°
Диаметр известен, 27 см.
Найдем угол между радиусами.
Он вдвое больше угла против основания.
(Вписанный угол равен половине центрального, опирающегося на ту же дугу.)
Угол против основания 180-70*2=40
Угол искомой дуги 40*2=80
L =27п *80°/360° =6п (см)
по теореме Пифагора: 4х^2 = x^2 + 225
3х^2 = 225
x^2 = 75
x = 10√3 - сторона треугольника
а) так как равносторонний треугольник - правильный треугольник, радиус описанной окружности = сторона / √3
R (описанной) = 10√3 / √3 = 10
r (вписанной) = R*cos 180/3 = 10* cos60 = 10 * 1/2 = 5