Дано: ABCA₁B₁C₁ - прямая призма с равными рёбрами. F∈A₁C₁; A₁F = FC₁
BC₁∩CB₁ = O
Найти: FO.
Боковые грани призмы это квадраты т.к. рёбра равны и призма прямая.
Пусть M∈B₁C₁ и OM⊥B₁C₁ тогда OM - медиана (т.к. ΔB₁O₁C₁ - равнобедренный), то есть B₁M = MC₁ значит FM - средняя линия ΔA₁C₁B₁.
FM = A₁B₁:2 = 4:2 см = 2см - как средняя линия.
MO = MB₁ - как катет в прямоугольном Δ с острым углом в 45° (ΔB₁OM).
MO = B₁C₁:2 = 4:2 см = 2см.
FM ⊥ MO т.к. призма прямая, то есть линейный угол, двугранного угла между основаниями и боковыми гранями, будет 90°.
По теореме Пифагора в прямоугольном ΔFMO:
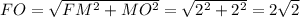 см.
см.
ответ: 2√2 см.
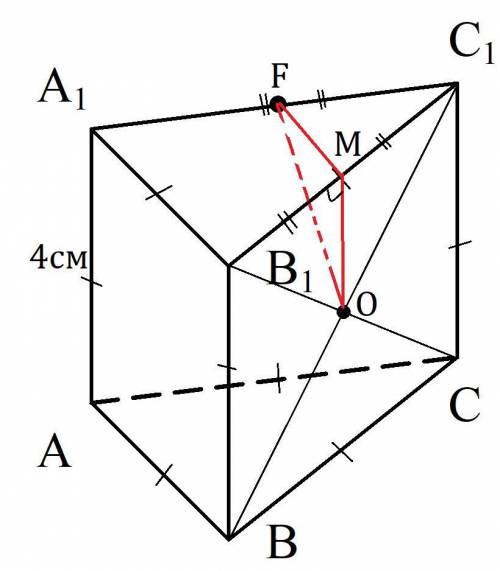
треугольник CDH прямоугольный. угол CDH=30 градусов => что CH=1/2 CD.
пусть CH=x ,тогда CD=2х. AB -высота. СН=АВ. АВ+CD=36 получаем что CD+CH=36. значит x+2x=36. отсюда х=12. высота найдена. найдем боковую сторону: 36-CH. СD=36-12=24. тк треугольник CDH прямоуг. тогда DH найдем по теореме пифагора: DH^{2}=CD^{2}-CH^{2}. получаем DH^{2}=24^{2}-12^{2}=576-144=432. DH=12\sqrt{3}. найдем нижнее(оно же большее основание) 8\sqrt{3}+12\sqrt{3}=20\sqrt{3}. найдем площадь трапеции: S=1/2*AD*BC. S= 1/2*8\sqrt{3}*20\sqrt{3}=240.
ответ: площадь S=240, высота AB=12.
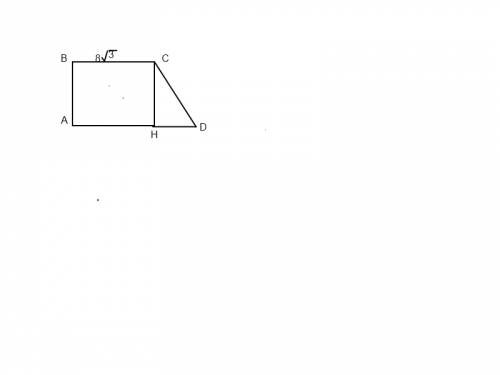
Т.к. угол между диагоналями прямоугольника равен 60 град, то значит и угол между основанием и диагональю прямоугольника равен 60 град, тогда
примем основание прямоугольника = а, высота прямоугольника (вторая сторона) = в, диагональ прямоугольника = с= 8см
тогда
cos60=а/с
а=с*cos 60=8*1/2=4 см
тогда
с^2=a^2+в^2
в^2=c^2-a^2=8^2-4^2=64-16=48 см
в=6,93 см
S=а*в=4*6,93=27,7 см^2