1. Расстояние от точки до прямой - это перпендикуляр к прямой. Наклонные к прямой и этот перпендикуляр образуют два прямоугольных треугольника. с гипотенузами, равными 13см и 15см и катетами, равными Х и Х+4. Второй катет - искомое расстояние - общий. Тогда по Пифагору можем написать: 13²-х² = 15²-(х+4)². Отсюда х=5см. Искомое расстояние равно: √(169-25) = 12 см.
2. Так как диагональ АС равнобокой трапеции АВСD образует с боковой стороной CD угол АСD, равный 90°, то большее основание трапеции AD является диаметром описанной окружности и равно 2R. В прямоугольном треугольнике ACD: Sinα = CD/AD => CD=2R*Sinα, а AC=2R*Cosα. Высота трапеции СН - это высота треугольника ACD, опущенная из прямого угла и по свойству этой высоты, равна: АС*СD/AD или СН=4R²Sinα*Cosα/2R = 2RSinα*Cosα. Но по формуле приведения 2Sinα*Cosα =Sin2α. Тогда ответ:
СН = RSin2α.
S = 1,125 ед².
Объяснение:
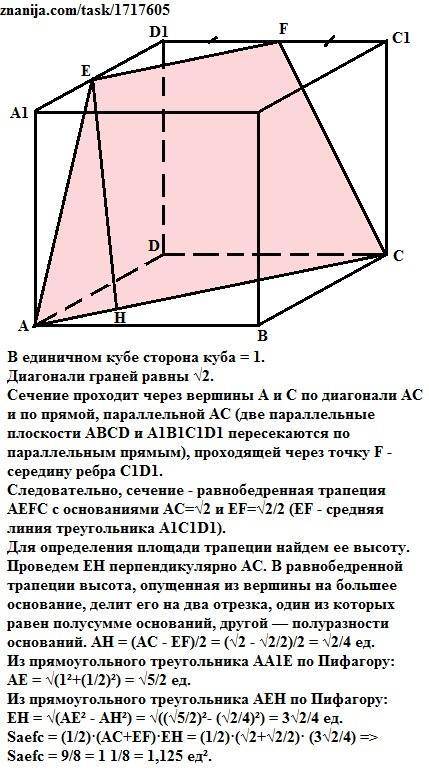
В единичном кубе сторона куба = 1.
Диагонали граней равны √2.
Сечение проходит через вершины А и С по диагонали АС и по прямой, параллельной АС (две параллельные плоскости ABCD и A1B1C1D1 пересекаются по параллельным прямым), проходящей через точку F - середину ребра С1D1.
Следовательно, сечение - равнобедренная трапеция AEFC с основаниями АС=√2 и EF=√2/2 (EF - средняя линия треугольника А1C1D1).
Для определения площади трапеции найдем ее высоту.
Проведем ЕH перпендикулярно АС. В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. АН = (АС - EF)/2 = (√2 - √2/2)/2 = √2/4 ед.
Из прямоугольного треугольника AА1Е по Пифагору:
АЕ = √(1²+(1/2)²) = √5/2 ед.
Из прямоугольного треугольника AЕН по Пифагору:
ЕН = √(АЕ² - АН²) = √((√5/2)²- (√2/4)²) = 3√2/4 ед.
Saefc = (1/2)·(AC+EF)·EH = (1/2)·(√2+√2/2)· (3√2/4) =>
Saefc = 9/8 = 1 1/8 = 1,125 ед².
Пусть АВ=а, А1В1=b, тогда а=3/√2=3√2/2 см и b=1/√2=√2/2 см.
О1К⊥А1В1 и КМ⊥А1В1, значит ∠О1КМ=120°. О1К║ОМ ⇒ ∠КМО=180-120=60°.
ОМ=а/2=3√2/4 см, О1К=b/2=√2/4 см.
КН⊥ОМ. МН=ОМ-ОН=ОМ-О1К=3√2/4-√2/4=√2/2 см.
В прямоугольном тр-ке КМН КМ=МН/cos60=√2 cм.
Площадь боковой поверхности состоит из четырёх равных трапеций, представляющих боковые грани пирамиды, значит площадь можно записать следующим образом:
Sб=4h(a+b)/2=2h(a+b), где h - высота боковой грани. h=КМ.
Sб=2√2(3√2/2+√2/2)=(2√2)²=8 см² - это ответ.