Периметр параллелограмма равен 90 см и острый угол равен 60 градусов. диагональ параллелограмма делит его тупой угол на части в отношении 1: 3. найти длину большей стороны параллелограмма.

👇

Ответ:

yanazyaka

18.06.2022

Из условия следует, что одна из диагоналей делит параллелограмм на два треугольника с углами 90, 60, 30 градусов (в чем нетрудно убедиться, построив рисунок). Тогда одна из соседних сторон параллелограмма больше другой в 2 раза, а их сумма равна 45. Тогда большая сторона 30.

4,8(46 оценок)

Открыть все ответы

Ответ:

marinaschakina

18.06.2022

11. Вроде как сумма всех внешних углов равна 900 градусов. (360*3-180(сумма всех внутренних углов треугольника). 360-60 = 300 - внешний угол того что 60 градусов. 900 - 300 = 600 градусов осталось. Т.к. один в двое больше другого, то они равны 200 и 400 соответственно. А разность = 200 градусов.

12. Если это диаметры одной и той же окружности (а как известно диаметр проходит через центр) то они не могут быть параллельны.

13. $\left \{ {{x + y=90} \atop {x/2=y/3}} \right.;\left \{ {{x=90-y} \atop {(90-y)/2=y/3}} \right.;\left \{ {{x=90-y} \atop {45 - y/2=y/3}} \right.;\left \{ {{x=90-y} \atop {45=y/3+y/2}} \right.;\left \{ {{x=90-y} \atop {270=5y}} \right.;\left \{ {{x=36} \atop {y=54}} \right.$ ,
где x и y углы.

14. представим угол А за Х;
x + 5х + x + 40 = 180;
7x = 140;
x = 20 градусов.
соответственно угол А = 20; угол В = 60 градусов, а угол С = 100 градусов.

15. Так как BD - это высота, то углы BDC и BDA прямые. Также BD - биссектриса угла MDH. Следовательно углы HDC и MDA равны. А так как треугольник ABC - равнобедренный, то и отрезки HC и MA равны. Но все равно желательно нарисовать.

16. Общий угол при пересечении прямых = 180 градусов. Значит второй угол у одной из параллельных прямых равен 180 - 112 = 68 градусов. У второй параллельной прямой то же самое только зеркально отображено. Тоже желательно нарисовать.

17. Треугольник АВС является равнобедренным. А у него углы у основания одинаковые. А так как углы CAD и BAC равны, то можно прийти к выводу что и стороны у этой фигуры равны. Но это не обязательно квадрат.

Хух.

4,4(14 оценок)

Ответ:

danilhgg52

18.06.2022

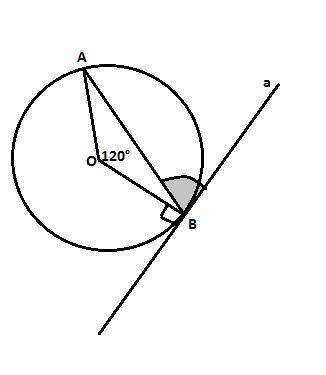
Угол между хордой и касательной равен половине градусной меры дуги, стягиваемой этой хордой (свойство), то есть половине градусной меры дуги АВ.

На дугу АВ опирается центральный угол АОБ, значит дуга АВ = 120°. Значит угол между касательной и хордой в точке касания равен 120°:2 = 60°

ответ: искомый угол равен 60°.

Или так:

В равнобедренном треугольнике АОВ (стороны ОА и ОВ равны - радиусы) углы при основании равны по (180-120):2=30° (сумма углов треугольника = 180°). Касательная в точке касания перпендикулярна радиусу, значит искомый угол равен 90° - 30° = 60°.

ответ: 60°