★☆★ Чертёж смотрите во вложении ★☆★
Дано:
Отрезки АМ и ВК пересекаются в точке О.
Точка О — серединная точка для отрезков АМ и ВК (ОА = ОМ ; ОВ = ОК).
Доказать:
АВ║МК.
Доказательство:
ⵈ◊ⵈ Для седьмого класса ⵈ◊ⵈ
Соединим точки А и В отрезком АВ ; точки В и М отрезком ВМ ; точки К и М отрезком КМ ; точки А и К отрезком АК.
Рассмотрим ΔАОВ и ΔМОК.
ОА = ОМ (по условию).
ОВ = ОК (по условию).
∠АОВ = ∠МОК (как вертикальные).
Следовательно, ΔАОВ = ΔМОК по двум сторонам и углу между ними (первый признак равенства треугольников).
▸В равных треугольниках против равных сторон лежат равные углы◂
ОВ = ОК.
Следовательно, ∠ВАО = ∠ОМК.
Рассмотрим прямые АВ и МК при секущей АМ.
▸Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны◂
Накрест лежащие ∠ВАО = ∠ОМК (по выше доказанному), следовательно, АВ║МК (по выше сказанному).
ⵈ◊ⵈ Для восьмого класса ⵈ◊ⵈ
Соединим точки А и В отрезком АВ ; точки В и М отрезком ВМ ; точки К и М отрезком КМ ; точки А и К отрезком АК.
Рассмотрим получившиеся выпуклый четырёхугольник АКМВ.
АМ и ВК — диагонали.
▸Если диагонали выпуклого четырёхугольника точкой пересечения делятся пополам, то такой четырёхугольник — параллелограмм◂
ОА = ОМ (по условию).
ОВ = ОК (по условию).
Следовательно, четырёхугольник АКМВ — параллелограмм.
▸Параллелограмм — четырёхугольник, противоположные стороны которого параллельны ◂
Поэтому, по выше сказанному —
АВ║МК ; АК║ВМ
Объяснение:
ответ: Р=6√2+2√14 или 15,8
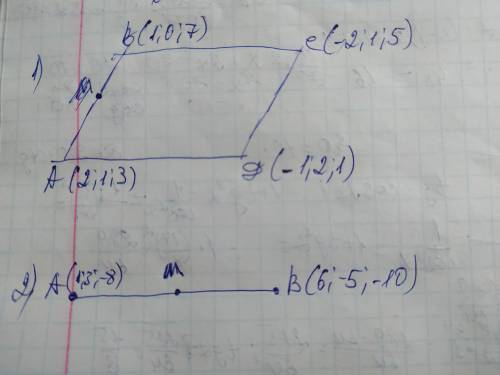
Объяснение: ЗАДАНИЕ 1
чтобы найти периметр параллелограмма нужно найти длины двух его сторон например АВ и ВС по формуле: АВ²=(Ах-Вх)²+(Ау-Ву)²+(Аz-Bz)²=
=(2-1)²+(1-0)²+(3-7)²=1²+1²+(-4)²=2+16=18;
AB=√18=3√2;
Точно так же найдём длину стороны ВС:
ВС²=(1-(-2))²+(0-1)²+(7-5)²=(1+2)²+1²+2²=
=3²+1+4=9+5=14; ВС=√14
СД²=(-2-(-1))²+(1-2)²+(5-1)²=(-2+1)²+(-1)²+4²=
=(-1)²+1+16=1+17=18; СД=√18=3√2;
АД²=(2-(-1))²+(1-2)²+(3-1)²=(2+1)²+(-1)²+2²=
=3²+1+4=9+5=14; АД=√14
Мы нашли все 4 стороны, но достаточно двух.
Все стороны совпадают и теперь найдём периметр параллелограмма.
Р=АВ+ВС+СД+АД=2×3√2+2×√14=
=6√2+2√14. Разные корни не прибавляются, и можно оставить так, но можно найти приблизительное значение корней и найти нужное число, округлив до десятых: √2≈1,4; √14≈3,7, получим:
6×1,4+2×3,7=8,4+7,4=15,8
ЗАДАНИЕ 2
Так как точка М- середина отрезка АВ, то её координаты найдём по формуле:
Мх=(Ах+Вх)/2=(1+6)/2=7/2=3,5
Му=(Ау+Ву)/2=(3-5)/2= -2/2= –1
Мz=(Az+Bz)/2=(-8-10)/2= –18/2= –9
ОТВЕТ: M(3,5; -1; -9)