Дано: угол cab=42 градуса найти: угол aco рисунок 740

Question

Геометрия: Дано: угол cab=42 градуса найти: угол aco рисунок 740

bodnari2121bodn · Accepted Answer

а) (-2;0) - центр окружности, радиус окружности равен 3.

б) (0; 4) - центр окружности, радиус окружности равен 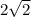$2\sqrt{2}$ .

в) (5; -7) - центр окружности, радиус окружности равен 4.

Объяснение:

Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.

а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.

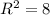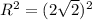
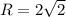б) (0; 4) - центр окружности, R^2=8 , $R^2=(2\sqrt{2})^2$ $R=2\sqrt{2}$ .

в) (5; -7) - центр окружности, R²=16, 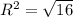$R^2=\sqrt{16}$ , R=4.

Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень