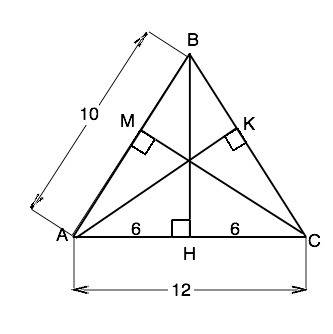
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
105°
Объяснение:
Для того, щоб знайти градусну міру двох суміжних кутів, якщо відомо, що різниця цих кутів дорівнює 30 °.
Для вирішення завдання складемо і вирішимо рівняння. І почнемо ми з вами з введення змінної x ° градусну міру меншого кута, тоді (x + 30) ° градусна міра більшого кута.
Для складання рівняння ми будемо використовувати теорему про суму кутів трикутника. В якій говориться, що сума суміжних кутів дорівнює 180 °.
x + (x + 30) = 180;
x + x + 30 = 180;
2x = 180 - 30;
2x = 150;
x = 75 ° менший кут і (75 + 30) = 105 ° більший кут.
2х из них- 88
Решение:
1. 360-88=272
т.к вертикальные углы равны, то
2. 272/2=136
это 3 и 4 углы.
3. 88/2= 44
это 1 и 2 углы
ответ: 1=2=44 и 3=4=136