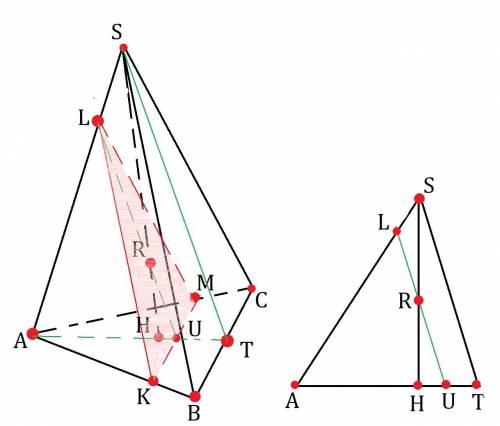
a) K, L, M ∈ α; α║(SBC)
KL║BS; KM║BC; ML║CS как линии пересечения двух параллельных плоскостей с одной общей.
SH⊥(ABC); AT⊥BC; H∈AT как центр правильного треугольника лежащий на медиане. AH:HT=2:1 по свойству пересечения медиан.
LU⊥KM ⇒ KU=UM ⇒ U∈AT ⇒ LU⊂(AST) ⇒ LU∩SH
Рассмотрим плоскость AST.
LU║ST как линии пересечения двух параллельных плоскостей с (AST).
AK:KB=AL:LS=5:1 по теореме о пропорциональных отрезках.
AU:UT=AL:LS по теореме о пропорциональных отрезках.
Как уже известно AH:HT=2:1. Пусть AU=5x; UT=x ⇒AT=6x ⇒ AH=4x; HT=2x ⇒ HU=2x-x=x.
ΔSHT~ΔRHU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит SH:RH=HT:HU=2:1. Пусть SH=2y; RH=y ⇒ SR=2y-y=y ⇒ SR=y=RH
То есть плоскость делит высоту пополам.
б) AT=AB*sin 60°=(15+3)*√3/2=9√3.
ΔAST~ΔALU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит AL:AS=LU:ST=6:5.
HT=1/3 *9√3=3√3 т.к. AH:HT=2:1
SH=13 ⇒ ST=√(169+27)=14 ⇒ LU=5/6 *14=35/3.
ΔAKM~ΔABC по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит KM:BC=AK:AB=5:6 ⇒ KM=5/6 *18=15.
Как было указано в начале LU⊥KM ⇒ S=1/2* 15*35/3=175/2=87,5
ответ: 87,5.
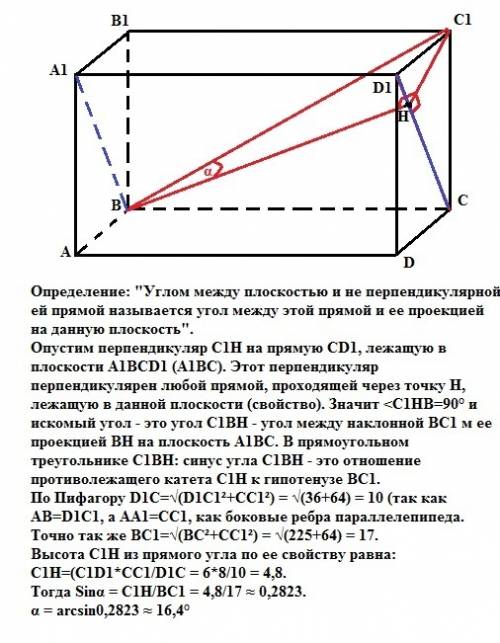
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
∠SMO = ∠MSO, также ∠MOS = 90°, тогда ∠SMO =
S(п.пов) = S(бок.бов) + S(осн).
S(бок.бов) =
S(осн.) = 4 * 4 = 16.
S(п.пов)