Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
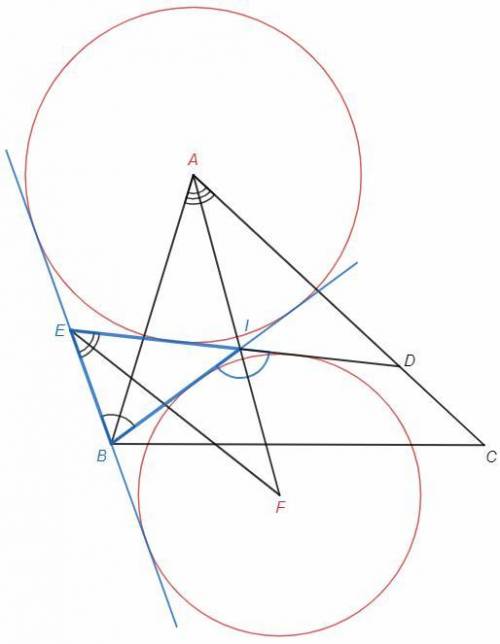
Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI

AA₁=√AB²-BA₁²=√a²-(a/2)²=a√3/2
S₁=AA₁·BC/2=a²√3/4 (площадь нижнего основания)
AO=(2/3)AA₁=a√3/3 OA₁=(1/3)AA₁=a√3/6 (так как медианы, пересекаясь, точкой пересечения делятся 2:1)
tgSAO=SO/AO, SO=AO*tdSAO=a√3/3*1/√3=a/3
OB₁=OA₁=a√3/6
SB₁=√SO²+OB₁²=√(a/3)²+(a√3/6)²=√a²/9+a²·3/36=a√1/9+1/12=a√7/6
S₂=AC·SB₁/2=a·a√7/(6·2)=a²√7/12 (площадь боковой грани)
S=S₁+3S₂=a²√3/4+3a²√7/12=(√3+√7)a²/4