ч. т. д.
Объяснение:
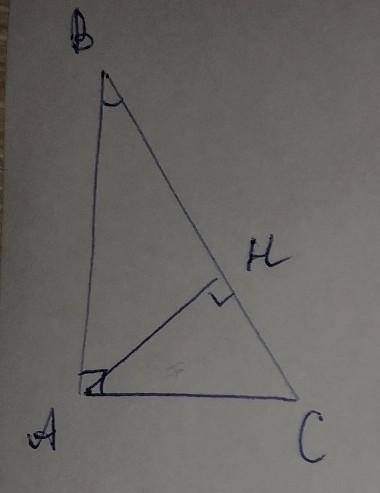
Дано: треугольник АВС, угол ВАС=90°, АН - высота.
Доказать: 4АН=ВС
Доказательство:
1. Рассмотрим тр-к АВС (угол А=90°): sinABC=sin15°=AC/BC, тогда BC=AC/sin15°;
2. Тр-к ВАС подобен тр-ку АНС по двум углам (т. к. АН - высота, угол АНС=90°=уголВАС; угол ВСА - общий).
Из подобия тр-ков следует равенство соответствующих углов: уголНАС=уголАВС=15°
3. Рассмотрим тр-к АНС (уголАНС=90°): cosHAS=cos15°=AH/AC, следовательно, AC=AH/cos15°.
4. АН/ВС=АН/(АС/sin15°)=AH/((AH/cos15°)/sin15°) =sin15°cos15°=2sin15°cos15°/2=sin30°/2=0,5/2=0,25
AH/BC=0,25=1/4, следовательно, 4АН=ВС
ч. т. д.
ответ: Р=36 см .
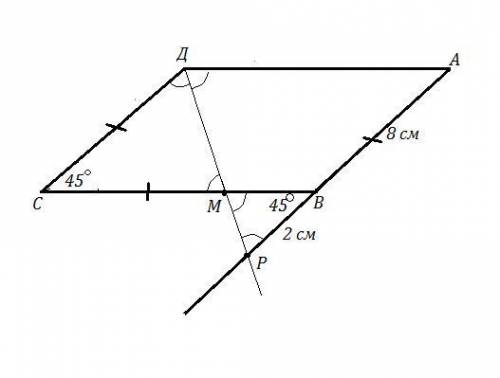
АВСД - параллелограмм , ДР - биссектриса, ∠С=45° ,
ДР пересекает АВ в точке Р , а ВС в точке М .
АР=10 см , ВР=2 см ⇒ АВ=10-2=8 см , СД=АВ=8 см как противоположные стороны параллелограмма .
ДР - биссектриса ⇒ ∠СДР=∠АДР .
∠АДР=∠СМД как накрест лежащие углы при АД || ВС и секущей ДР .
В ΔСМД два угла равны ⇒ ΔСМД - равнобедренный и СМ=СД=8 см ∠СМД=(180°-45°):2=67,5°
∠ВМР=∠СМД=67,5° как вертикальные .
В ΔВМР угол ∠МВР=45° , так как ∠МВР=∠МСД=45° как накрест лежащие углы при АР || СД и секущей ВС .
Но тогда в ΔВМР: ∠ВРМ=180°-45°-67,5°=67,5° , то есть ΔВМР есть два равных угла: ∠ВМР=∠ВРМ=67,5° , тогда этот треугольник равнобедрен-ный и ВМ=ВР=2 см .
Тогда ВС=СМ+ВМ=8 +2 =10 см , АД=ВС=10 см
Периметр Р=10+10+8+8=36 см .
Прямоугольные тр-ки АДВ и АЕВ равны т.к. ∠ДАВ=∠ЕАВ и сторона АВ общая, значит АД=АЕ.
В равнобедренном треугольнике АДЕ угол при вершине равен 60°, значит он правильный, вписанный в окружность с центром в точке О и радиусом R.
Для правильного тр-ка R=a/√3 ⇒ a=R√3.
Хорды АД и АЕ равны а.
ответ: R√3.