2,47м BG=54см, AH=64см. Учите геометрию (мастер ее в школе выучил)
Объяснение:
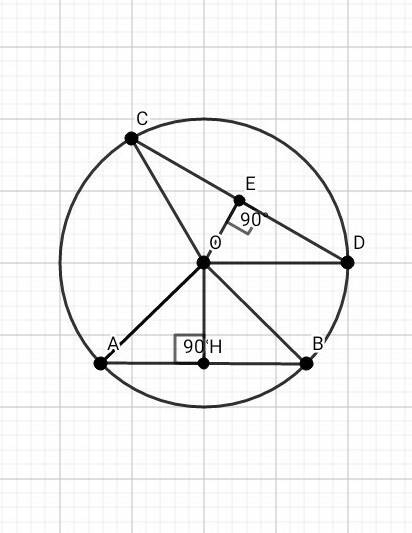
Поскольку AH, BG, CF, DЕ параллельны, то ABGH, BCFG, CDEF - трапеции. Раз EF=FG=GH, то и DC=BC=AB по теореме Фалеса. Кроме того, CF является средней линией трапеции BDEG, а BG - средней линией трапеции ACFH. Средняя линия трапеции равна полусумме оснований.
EF=FG=GH=10cm
AB=DC=CD=7cm
DE=34cm, CF=44cm Тогда BG=54cm (CF=(DE+BG)/2, BG=2CF-DE=2*44-34=54)
2BG=CF+AH, AH=2BG-CF=2*54-44=64cm
AB+BC+CD+DE+EF+FG+GH+AH+BG+CF=7+7+7+34+10+10+10+64+44+54=247см=2,47м
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Теорема 3. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Объяснение:
Дано: окружность с центром О. АВ и СД - хорды, АВ=30, КО=20; МО=15. Найти СД.
Решение: КО⊥АВ и МО⊥СД, т.к. перпендикуляр - кратчайшее расстояние между точкой и прямой. Треугольники АОВ и СОД - равнобедренные, причем АО=ОВ=ОС=ОД как радиусы окружности.
Рассмотрим ΔАОВ; КО - высота и медиана, поэтому АК=КВ=АВ:2=30:2=15. Найдем ОВ из ΔОКВ; ОВ=25, т.к. ΔОКВ - "египетский".
Рассмотрим ΔДОМ; ОМ - высота и медиана, поэтому СМ=ДМ. ОД=ОВ=25, ОМ=15, значит, ДМ=20 (по свойству египетского треугольника). СД=СМ+ДМ=20+20=40 (ед.)
ответ: 40.