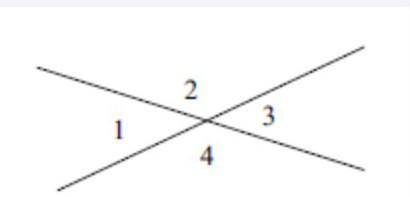
Решение, а) По условию Z2 + Z4 = 220°. Эти углы вертикальные, поэтому Z2 = Z4 = 110°.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°, откуда Z1 = 180° -- 110° = 70°.
Углы 3 и 1 вертикальные, поэтому Z3 = Z1 = 70°.
б) Углы 1 и 3, а также 2 и 4 вертикальные, поэтому Z3 = Zl, Z4 = = Z2. Подставив эти выражения в данное равенство, получим:
3(2Z1) = 2Z2,
или
3Z1 =Z2.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°. Из этих двух равенств находим Z1 и Z2: Z1 = 45°, Z2 = 135°.
Z3 = Z1, поэтому Z3 = 45°; Z4 = Z2, поэтому Z4 = 135°
в) По условию Z2 — Z1 = 30°. Эти углы смежные, следовательно, Zl + Z2 = 180°. Из этих двух равенств имеем: Z1 = 75°, Z2 = 105°.
Z3 = Z1, поэтому Z3 = 75°; Z4 = Z2, поэтому Z4 = 105°.
ответ, a) Zl = Z3 = 70°, Z2 = Z4 = 110°; б) Zl =Z3 = 45°, Z2 = = Z4 = 135°; в) Zl = Z3 = 75°, Z2 = Z4 = 105°.
---. ---.---.---.---.
Сколько целых значений x удовлетворяют неравенству
- 5< |-x| ≤ 3 ?
- 5< |-x| ≤ 3 ⇔ - 5< |x| ≤ 3. двойное неравенство заменяем системой неравенств ⇔
{ |x | > - 5 ; |x| ≤ 3. ⇔ { -∞ < x <+∞ ; - 3 ≤ x ≤ 3. ⇒ - 3 ≤ x ≤ 3.
целые значения x из этого интервала { - 3 ; - 2 ; -1; 0 ; 1; 2; 3 }
ответ : 7.
* * * * * * * *
P.S.
| -x| = |x| * * * например | -17 | = 17 и |17| = 17 * * *
| x | ≥ 0 верно для всех x , поэтому решение неравенства |x| > - 5 есть ( -∞ ; ∞).