2,5
Объяснение:
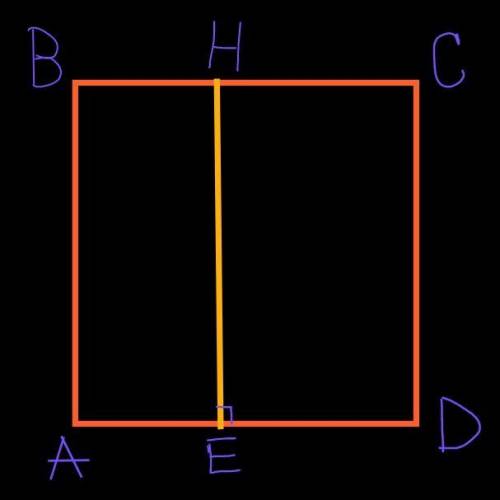
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5
2,5
Объяснение:
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5

Сторона квадрата вписанного в круг равна : Sqrt(r^2 + r^2) = Sqrt(2r^2) = r*Sqrt(2) , Значит ребро вписанного куба равно : r*Sqrt(2) , и соответственно и высота цилиндра будет равна : r*Sqrt(2) . Объем цилиндра равен : п* r^2 *r * Sqrt(2) = п *r^3 *Sqrt(2) .По условию задачи имеем , что объем цилиндра равен : 54*п см^3 , то есть : п* r^3 * Sqrt(2) = 54*п
r^3 * Sqrt(2) = 54
r^3 = 54 / Sqrt(2)
Объем вписанного куба в цилиндр равен : (r*Sqrt(2))^3 = 2r^3 * Sqrt(2)
Подставляем полученное значение радиуса цилиндра , Получаем :
Объем вписанного в цилиндр куба равен : 2 * 54/Sqrt(2) * Sqrt = 2 * 54 = 108 см^3