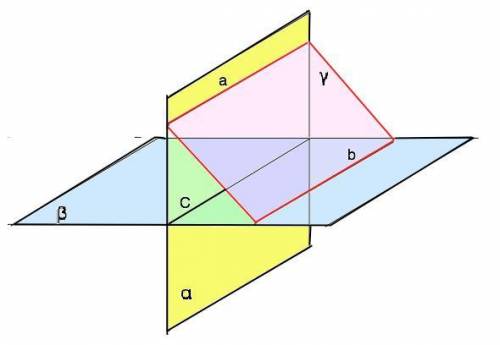
Если плоскость проходит через данную прямую , параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Плоскость α проходит через прямую С, параллельную плоскости γ, и пересекает эту плоскость, => линия пересечения а плоскостей α и γ параллельна прямой С. => а||С
Из теоремы о параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Прямая а не лежит в плоскости β и параллельна прямой С, лежащей в плоскости β, значит, прямая а параллельна плоскости β.
Аналогично плоскость β проходит через прямую С, параллельную плоскости γ, пересекает плоскость γ, => линия пересечения b плоскостей β и γ параллельна прямой С. => b || С, значит, b || α.
Доказано.
ответ: 24
Объяснение:
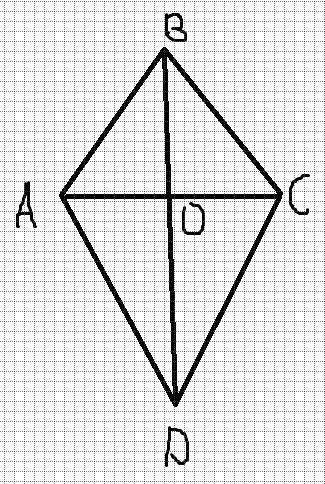
Смотри рисунок визуально становиться понятно что на против большее диагонали лежит больший угол то есть углы BAD=BCD=120 градусов, а так как углы ромба в сумме должны давать 360 и противоположные углы равны то углы ABC=CDA=60 градусов 360-240=120/2=60 из условия задачи мы знаем что AC=6 см. А еще у ромба есть такое свойство: Диагонали являются биссектрисами то есть углы ADO=ODC=ABO=OBC=30 градусов, а углы DAO=OAB=BCO=OCD=60 градусов соответственно. Есть такое своистово в прямоугольном треугольнике что напротив угла в 30 градусов располагается катет равный половине гипотенузы. Это свойство нам найти сторону ромба, а после зная сторону мы найдем периметр по формуле 4* на длинну стороны, кстати стороны у ромба равны вот. В нашем случае AO=1/2*AD так как AO лежит напротив угла прямоугольного треугольника AOD равного 30 градусов. Так как AD=DC=CB=AB, а углы DAC и ACD равны 60 градусов то треугольник ADC является равнобедренным. А у равнобедренных треугольников биссектриса, проведенная к основанию, является медианой и высотой. А так как угол AOD равен 90 градусов то OD есть не что иное, как высота биссектриса и медиана данного треугольника, а если она медиана то она делит AC пополам значит AO=6/2=3 значит AD=3*2=6, а периметр в итоге равен 6*4=24