Обратим внимание на то, что речь идет о противоположных углах, а не об углах, прилежащих к одной боковой стороне трапеции. Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние при пересечении параллельных прямых секущей.
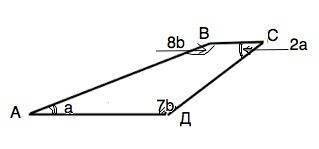
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b – а, т.к. они равны.
Тогда а+8а=180°⇒
а=20° и b=20°.
Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.
Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние.
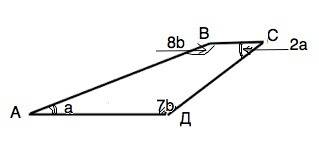
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b - а
Тогда а+8а=180°⇒
а=20°. Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.
Пирамида правильная, значит, её основание - квадрат, а вершина проецируется в точку пересечения диагоналей. Обозначим пирамиду МАВСD. МО - её высота, ОН - проекция апофемы МН. МН⊥АВ, ⇒ ОН⊥АВ ( по ТТП) КН параллельна и равна ВС, ОН=КН:2=75 см.
Треугольник МОН – прямоугольный. По т.Пифагора апофема МН=√(MO²+OH²)=√(40²+75²)=85 см
Площадь поверхности крыши равна площади 4-х боковых граней. 4•S(AMB)=4•МН•АВ:2=2,55 м²⇒ Вес крыши песочницы 78•2,55=198,9 кг