Основание пирамиды прямоугольник со сторонами 6см и 7 см все боковые ребра равна 13 см найдите обьем пирамиды

👇

Ответ:

elisavetto4ka

06.05.2022

Формула объёма пирамиды:
V=(1/3)*S*H
S - площадь основания
H - высота пирамиды

Так как нам известно, что в основании лежит прямоугольник, а его стороны 6 и 7, то сразу найдём площадь основания:
S=a*b=6*7=42

Теперь нужно найти высоту. Для этого нам нужно найти диагональ прямоугольника. Воспользуемся теоремой Пифагора
d=√(7²+6²)=√85

Теперь рассмотрим треугольник, образованный высотой пирамиды, её гранью и половиной диагонали основания. С теоремы Пифагора найдём высоту
H=√(13²-(√(85)/2)²)=√111
V=(1/3)*42*√111=14√111

4,4(14 оценок)

Открыть все ответы

Ответ:

Рома67463

06.05.2022

ответ: стороны треугольника 13; 14; 15

Объяснение: проведенные отрезки - это биссектрисы данного треугольника (центр вписанной окружности - точка пересечения биссектрис треугольника);

получившиеся треугольники имеют равные высоты - это радиус вписанной окружности (любая точка биссектрисы угла равноудалена от сторон угла; радиус, проведенный в точку касания перпендикулярен касательной)

площади треугольников, имеющих равные высоты относятся как основания; получим отношения сторон треугольника (для определенности обозначим сторону (а) у треугольника с площадью 30; сторона (b) у треугольника площадью 28; (с) для площади 26):

а/b = 30/28 = 15/14

a/c = 30/26 = 15/13

b/c = 28/26 = 14/13

можно записать три стороны:

a = 15c/13; b = 14c/13 и с.

площадь всего треугольника = 30+28+26 = 84 и она связана со сторонами по формуле Герона)

полупериметр = ((15/13)+(14/13)+1)*(c/2) = 21c/13

84 = корень из((21с/13)*(6c/13)*(7c/13)*(8c/13))

84 = 7*3*4*c^2/169

c^2 = 169

c = 13

b = 14

a = 15

4,6(28 оценок)

Ответ:

Мариелла17

06.05.2022

Обозначим стороны как a;b

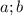. И пусть

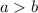тогда большая высота опускается на меньшую сторону , меньшая на большую . Тогда площадь с одной стороны равна S=3b

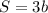, с другой стороны S=2a

.
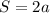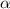Вспомним что угол между высотами проведенные с тупого угла равен острому углу параллелограмма.Учитывая это обозначим угол между высотами как $\alpha$ тогда острый угол равен 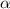$\alpha$ следовательно тупой 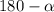$180- \alpha$ . Из прямоугольных треугольников которые образовались после проведения высота соответственно на стороны a ;b

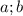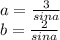равны $a=\frac{3}{sina}\\
b=\frac{2}{sina}$ тогда площадь запишится как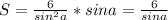
$S=\frac{6}{sin^2a}*sina=\frac{6}{sina}$
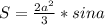но и она же равна $S=\frac{2a^2}{3}*sina$ приравняем
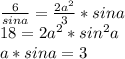$\frac{6}{sina}=\frac{2a^2}{3}*sina\\
18=2a^2*sin^2a\\
a*sina=3$ -3 нам не подходит потому что синус в I;II

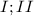четверти положителен
Диагональ выразим по теореме косинусов
$5^2=a^2+\frac{4a^2}{9}-2*a*\frac{2a}{3}*cos(180-a) \\
5^2=a^2+\frac{4a^2}{9}+\frac{4a^2}{3}*cosa\\
cosa=\frac{25-a^2-\frac{4a^2}{9}}{\frac{4a^2}{3}}\\
$
с первого равенство выразим синус через косинус затем подставим и решим уравнение перейдем в общем к такому
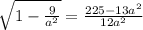$\sqrt{1-\frac{9}{a^2}}=\frac{225-13a^2}{12a^2}\\
$ решая это уравнение получим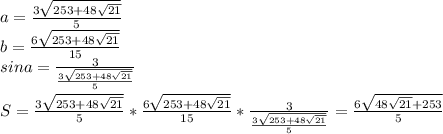
$
a=\frac{3\sqrt{253+48\sqrt{21}}}{5}\\
b=\frac{6\sqrt{253+48\sqrt{21}}}{15}\\
sina=\frac{3}{\frac{3\sqrt{253+48\sqrt{21}}}{5}}\\\\
S=\frac{3\sqrt{253+48\sqrt{21}}}{5}*\frac{6\sqrt{253+48\sqrt{21}}}{15}*\frac{3}{\frac{3\sqrt{253+48\sqrt{21}}}{5}}=\frac{6\sqrt{48\sqrt{21}+253}}{5}$
оно примерно равна 26

Найти площадь параллелограмма. если его наибольшая диагональ равна 5 см. а две его высоты, соответст