
Доказательство в объяснении.
Объяснение:
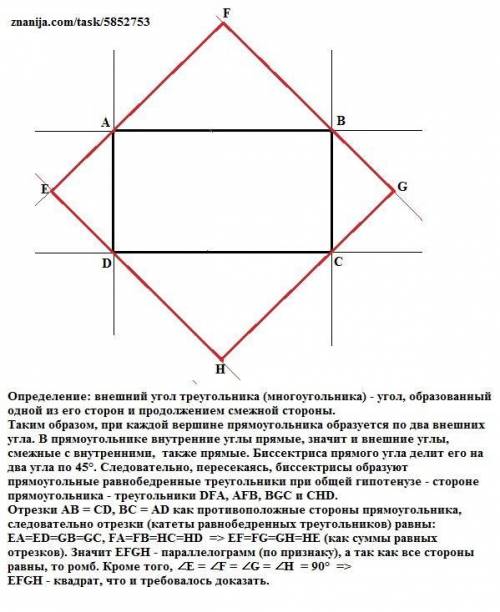
Определение: внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны.
Таким образом, при каждой вершине прямоугольника образуется по два внешних угла. В прямоугольнике внутренние углы прямые, значит и внешние углы, смежные с внутренними, также прямые. Биссектриса прямого угла делит его на два угла по 45°. Следовательно, пересекаясь, биссектрисы образуют прямоугольные равнобедренные треугольники при общей гипотенузе - стороне прямоугольника - треугольники DFA, AFB, BGC и CHD.
Отрезки АВ = CD, BC = AD как противоположные стороны прямоугольника, следовательно отрезки (катеты равнобедренных треугольников) равны: EA=ED=GB=GC, FA=FB=HC=HD => EF=FG=GH=HE (как суммы равных отрезков). Значит EFGH - параллелограмм (по признаку), а так как все стороны равны, то ромб. Кроме того, ∠E = ∠F = ∠G = ∠H = 90° =>
EFGH - квадрат, что и требовалось доказать.
АВСДА1В1С1Д1 - усеченная пирамида , в основаниях квадраты АВСД со стороной =10, А1В1С1Д1 со стороной=2, ОО1-высота пирамиды=7, АС=корень(АД в квадрате+СД в квадрате)=корень(100+100)=10*корень2, А1С1=корень(А1Д1 в квадрате+С1Д1 в квадрате)=корень(4+4)=2*корень2,
рассматриваем АА1С1С как равнобокую трапецию, АА1=СС1, проводим высоты А1К и С1Н на АС, КА1С1С-прямоугольник А1С1=КН=2*корень2, А1К=С1Н=ОО1=7-высота, треугольник АА1К=треугольник НС1С как прямоугольные по гипотенузе и катету, АК=СН=(АС-КН)/2=(10*корень2-2*корень2)/2=4*корень2
АН=АК+КН=4*корень2+2*корень2=6*корень2, треугольник АС1Н прямоугольный, АС1-диагональ пирамиды=корень(АН в квадрате+С1Н в квадрате)=корень(72+49)=11