(а) Площадь пола команды считаем в см 250х150=37500 см кв.
Считаем площадь одной плитки 30х30=900 см кв
ПЛ пола делим на ПЛ плитки 37500/900=41.666, округляем 42 плитки
(б) 3,2 (м) = 3,2*100 = 320 (см).
2,5 (м) = 2,5*100 = 250 (см).
Площадь прямоугольника равна произведению его смежных сторон.
Так как стена имеет форму прямоугольника, то его площадь равна -
250 (см)*320 (см) = 80000 (см²).
А площадь одной прямоугольной плитки равна -
20 (см)*10 (см) = 200 (см²).
Чтобы найти число плиток, площадь стенки разделим на площадь одной плитки -
80000 (см²) : 200 (см²) = 400 (плиток).
400 плиток.
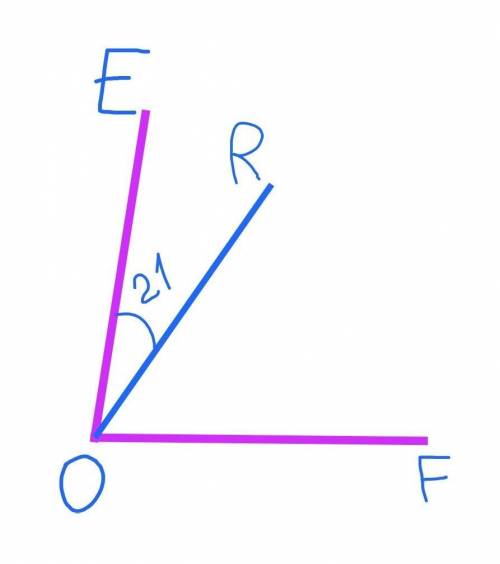
№1
Угол ЕОR=21° по условию
Угол ROF в 3 раза больше угла ЕОR, тогда угол ROF=21°*3=63°.
Угол ЕОF=угол EOR+угол ROF=21°+63°=84°
ответ: 84°
№2
Пусть длина ВС – х, тогда длина АС – 2х
АВ=АС+ВС;
15=2х+х
15=3х
х=5
Тогда длина ВС=5 см, а длина АС=2*5=10 см.
ответ: 10 см, 5 см
№3
а) Угол смежный углу КОЕ – это угол СОЕ (прямая СК и общая сторона ОЕ) или угол NOK (прямая NE и общая сторона ОК)
ответ: два варианта. Выбирай любой.
b) 1 пара: угол КОЕ и угол CON (пересекающиеся прямые СК и NE)
2 пара: угол СОЕ и угол KON (пересекающиеся прямые СК и NE)
c) Так как углы КОЕ и CON вертикальны, то они равны. Угол CON=46° по условию, тогда и угол КОЕ=46°.
d) Угол СОК – развернутый, тоесть он равен 180°;
Угол РОК=65° по условию;
Угол CON=46° по условию;
Угол PON=угол СОК–угол РОК–угол CON=180°–65°–46°=69°
ответ: 69°
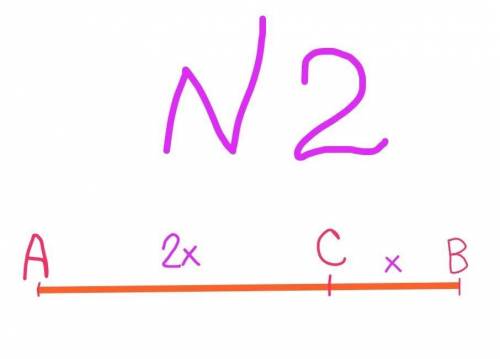
AA₁_|_α
BB₁_|_α
=> AA₁ || BB₁
A₁∈α, B₁ ∈α
A₁ABB₁ - трапеция.
AA₁=3 см
BB₁=11 см
A₁B₁=15 см
дополнительные построения: AK_|_BB₁
AK||A₁B₁, AK=15 см
AA₁=KB₁=3 см
BK+KB₁=BB₁, KB₁=8 см
прямоугольный треугольник:
катет АК=15 см
катет КВ=8 см
гипотенуза АВ, найти по теореме Пифагора:
АВ²=15²+8², AB²=289
AB=17 см