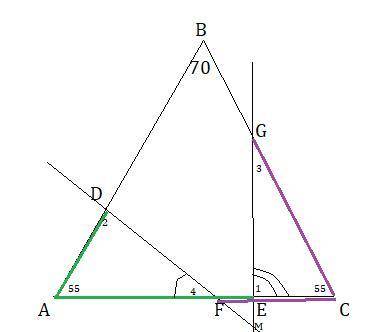
На основании равнобедренного треугольника отметили две различные точки F и E , а на боковых сторонах AB и –BC точки D и G соответственно так, что AD +AE = AC и CF+ CG = AC. Найти угол между прямыми DF и EG, если угол ABC = 70°.
Объяснение:
ΔАВС-равнобедренный,значит ∠А=∠В=(180°-70°):2=55°.
По условию АD+АЕ=АС и CF+ CG = AC ⇒АD=ЕС и AF=CG.
ΔADF ≈ΔCFG по 2 пропорциональным сторонам и равному углу между ними :∠А=∠В и AD/EC=AF/CG ⇒соответственные углы равны ∠1=∠2 ,∠3=∠4.
ΔFEM : найдем угол ∠М ; ∠Е=∠1, ∠F=∠4 . Сумма углов ∠F+∠Е=180°-55°=125° , тогда ∠М=180°-125°=55°
пирамида КАВСД, К-вершина, АВСД квадрат со стороной=4, КС перпендикулярно АВСД, две грани ВКС и ДКС перпендикулярны АВСД, уголКДС=уголКВС=60 -наклон граней АКД и АКВ к плоскости основания, треугольник КДС прямоугольный, угол ДКС=90-уголКДС=90-60=30, КД=2*СД=2*4=8, КС=КД*sin60=8*корень3/2=4*корень3,
треугольник ВКС=треугольник КДС как прямоугольные по двум катетам, площадьКДС=1/2*СД*КС=1/2*4*4*корень3=8*корень3=площадьКВС,
согласно теореме отрех перпендикулярах, КД перпендикулярно АД, а КВ перпендикулярно АВ,
треугольники АВК=треугольник АКД как прямоугольные по гипотенузе (АК-общая) и катету(АД=АВ), площадь АКД=1/2*КД*АД=1/2*8*4=16=площадь АКВ,
боковая поверхность=2*площадьКДС+2*площадьАКД=2*8*корень3+2*16=16*(корень3+2)
a-сторона
h-высота
a=S/h=12/2.4=5см
P=4a=20см